Code
par(mgp=c(4,1,0), mar=c(6,5,2,2))
xlab <- c(paste0('Pre-test\nvariance=', round(var(pre), 3)),
paste0('Post-test\nvariance=',round(var(post), 3)))
histbackback(pre, post, brks=seq(0.01, 0.99, by=0.01), xlab=xlab, ylab='Prob(CAD)')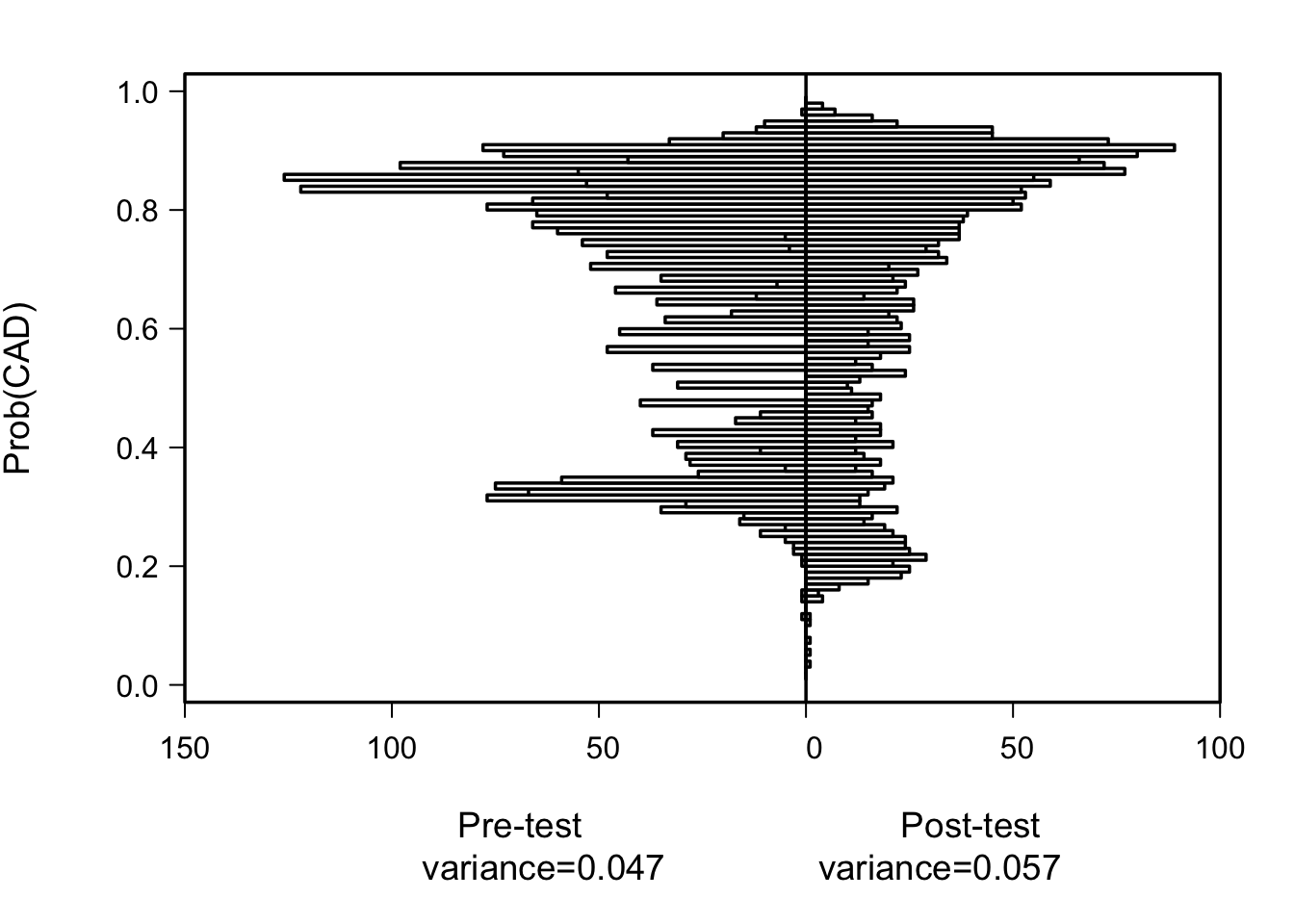
Department of Biostatistics
Vanderbilt University School of Medicine
October 17, 2018
When the outcome variable Y is continuous, there are only three measures of added value that are commonly used: increase in \(R^2\), decrease in mean squared prediction error, and decrease in mean absolute prediction error. Why have so many measures been invented when Y is binary or censored?
A recurring topic in clinical and translational research is the assessment of new information provided by molecular, physiologic, imaging, and other biomarkers. The notion of added value is in the predictive sense, either when diagnosing a hidden disease, e.g., predicting current status using a binary or ordinal logistic model, or when predicting future events, e.g., using a time-to-event statistical model to predict future disease occurrence, recurrence of disease, or occurrence of a clinical event such as death or stroke.
Before getting into purely analytical issues, note that there are many study design issues. One of the most common mistakes, sometimes intentional, is to fail to collect variables that are available in medical practice to put into the base model. This leads to inadequate adjustment for prior information, setting the bar too low when measuring added value of new information. Other common mistakes are categorizing some of the adjustment variables, resulting in residual confounding and failure to adjust for the real background variables, and categorizing new continuous measurements, resulting in understatement of their added value. Without knowing it, many translational researchers, by dichotomizing new biomarkers, are requiring additional biomarkers to be measured to make up for the lost information in dichotomized markers.
Statisticians have no better sense of history than other scientists. In the quest for publishing new ideas, measures of added value are constantly being invented by statisticians, without asking whether older methods already solve the problem at hand. Some of the examples of measures that are commonly used but are not needed in this setting are the \(c\)-index (F. E. Harrell et al. (1982); area under the ROC curve if the outcome is binary), and IDI and NRI. They are not needed because measures based on standard regression methods are not only adequate to the task, but are more powerful and more flexible and insightful, especially when interactions are involved. Especially problematic are measures such as the categorical version of NRI (net reclassification improvement) which not only requires arbitrary categorization of risk estimates but then goes on to use inefficient binary summaries from them. Pencina (personal communication) has regretted including statistical tests for these measures in his highly-cited paper, as these tests have nowhere near the power of the gold-standard likelihood ratio test.
Comparing two c-indexes (one from the base model and one from the larger model containing the new biomarkers) is a low-power procedure. This is because the c-index is a rank measure (the concordance probability from the Wilcoxon test or Somers’ \(D_{xy}\) rank correlation) that does not sufficiently reward extreme predictions that are correct1. And taking the difference between two c-indexes corresponds to taking the difference in two Wilcoxon statistics, which is never done. Instead, a head-to-head comparison is demanded. This can be done by using a different U-statistic based on all possible pairs of observations and counting the fraction of pairs for which one model is “more concordant” with the outcome than the other model. This respects pairings of pairings, and is implemented in the R Hmisc package rcorrp.cens function. Still, this is not as powerful as the likelihood ratio \(\chi^2\) test.
1 The Wilcoxon, Spearman, and other rank tests are very powerful for testing for existence of an association, but not for assessing differences in the strength of association.
Worse than any of these problems is the continued use of discontinuous improper accuracy scoring rules such as sensitivity, specificity, precision, and recall.
There are three gold standards, and statisticians have too often tried to forget them in the search for novelty:
Methods based on one of these gold standards are simpler, more powerful, and allow for greater complexity. The best example of handling complexity will be demonstrated in the case study below, in which the new marker interacts with a standard variable (there, age) when predicting disease probability.
In the binary outcome (Y) case, there are two commonly used proper accuracy scores: the logarithmic accuracy score (a per-observation log-likelihood), and the quadratic accracy score (Brier score; mean squared error). The log-likelihood can be turned into a 0-1 pseudo \(R^2\) measure: \(1 - \exp(-\text{LR} / n)\). The only thing going against pseudo \(R^2\) is the difficulty in interpreting its absolute value. But it is excellent for comparing two or more models, even though examining increases in LR is better.
Explained outcome variation is another key type of measure. In the linear model, the traditional \(R^2\) is often used. This is SSR / SST where SSR is the sum of squares due to regression (the sum of squares of differences between predicted values and the mean predicted value), and SST is the sum of squares total, which is n-1 times the variance of Y. \(R^2\) may also be written as SSR / (SSR + SSE) where SSE is the sum of squared residuals. In the linear model, \(R^2\) and the log-likelihood are measuring the same thing since LR = \(-n \log(1 - R^{2})\).
We can re-express \(R^2\) as \(\frac{\text{var}(\hat{Y})}{\text{var}(Y)}\) where \(\hat{Y} = X \hat{\beta}\) is the linear predictor (predicted mean, for the linear model).
\(R^2\) can equivalently be written as the ratio of the explained variance to the sum of explained and unexplained variance. The unexplained variance is the variance of the residuals in the linear model. For a probability model, the natural way to express the proportion of explained variance is through the predicted probabilities that Y=1, denoted by \(\hat{P}\). The \(R^2\) measure for a binary Y model is then \[\frac{\text{var}(\hat{P})}{\text{var}(\hat{P}) + \sum_{i}^{n} \hat{P}_{i} (1 - \hat{P}_{i}) / n}\] where \(\text{var}(\hat{P})\) is the sample variance of the \(n\) \(\hat{P}_{i}\).2
2 Schemper (2003) is an excellent paper advocating for measures based on absolute rather than squared differences.
Kent and O’Quigley (1988) have extended the idea of the fraction of explained variation in the outcome to various nonlinear models including those used in survival analysis. The SST or var(Y) is distribution-specific. The beauty of this approach is its focus on the variance of \(\hat{Y}\), which is independent of the prevalence of Y=1 in the binary case and of the amount of censoring in time-to-event analysis. See also B. Choodari-Oskooei, Royston, and Parmar (2012) and Babak Choodari-Oskooei, Royston, and Parmar (2012).
A different type of key measure will also be exemplified in the case study: differences in predicted values between the base model and the expanded model.
Relative explained variation is a simple concept that has the extra advantage of being completely free of the distribution of Y and the customized error variance or SST necessary for computing the proportion of explained variance for distributions other than the normal. For a linear model relative explained variation is the ratio of the \(R^2\) for the base model to the larger \(R^2\) for the combined model that contains also the new markers being tested. And since for \(R^{2} \leq 0.25\), \(-n \log(1 - R^{2})\) is approximately \(n R^{2}\), the relative variation explained by the base variables is approximately equal to the adequacy index discussed in the maximum likelihood estimation chapter of Regression Modeling Strategies (Frank E. Harrell (2015)): \[\text{Adequacy index} = \text{LR}_{A} / \text{LR}_{AB}\] where the base model is denoted by A, the added predictors (e.g., biomarkers) are denoted by B, AB represents the combined model with A and B as predictors, and LR is defined above. Here adequacy refers to the adequacy of the model that ignores the new predictors.
Whether using the adequacy index or relative variation explained, one minus such an index is the fraction of new information provided by predictors in B. It is the proportion of explainable variation that is explained by B.
To emphasize the simplicity of relative explained variation, it is just the ratio of variances of predicted values. And other statistical indexes may be computed from the predicted values, such as the mean absolute difference from the mean predicted value, and the \(g\) index described in Regression Modeling Strategies. The latter is the mean absolute difference between any two predicted values. But it is possible for the \(g\) index for AB to be smaller than that for model A.
A general-purpose way to compute relative explained variable for virtually any regression model is to use the linear model as a bridge to the current model. The linear model is fitted to the linear predictor (here the predicted log odds) developed from the model of interest. The linear model will exactly reproduce our model, with \(R^{2}=1.0\). Use the ordinary partial \(R^2\) from the linear model fit to estimate relative explained variation in the original model on the linear predictor scale. The R rms package rexVar function does these calculations, and if the model is a Bayesian model or was bootstrapped with the R rms bootcov function with coef.reps=TRUE uncertainty intervals for relative explained variation are also computed. Here is a full example for the new measure.
rexVar is available in rms 6.8-0Consider a series of patients from the Duke Cardiovascular Disease Databank. These patients were referred to Duke University Medical Center for chest pain and underwent cardiac catheterization during which a dye is injected and a coronary angiography is used to view blockages of coronary arteries. Significant coronary artery disease is here defined as a blockage of at least 75% by vessel diameter, in at least one major coronary artery. Here we consider total cholesterol as if it were a new diagnostic marker, and we wish to quantify the new diagnostic information provided by cholesterol. The base model is oversimplified for purposes of illustration. It contains only the powerful variables age and sex. In practice it should contain in addition to age and sex all relevant easily available baseline variables, such as pain characteristics, blood pressure, smoking history, etc. From previous analysis, a nonlinear interaction was demonstrated between age and sex and between age and cholesterol. The former is related to women “catching up” with men with respect to cardiovascular risk, after menopause. The latter interaction captures the fact that high cholesterol is not as dangerous for older patients and the possibility that very low cholesterol is actually harmful for them.
The dataset is available from the Vanderbilt Department of Biostatistics wiki, and includes 2258 patients with all variables measured. It may be automatically downloaded using the R Hmisc getHdata function. The dataset is also analyzed in the BBR diagnosis chapter and here. The latter link contains more analyses that compare pre- and post-test probabilities.
We first fit a binary logistic regression model with interactions, modeling age and cholesterol in a smooth nonlinear fashion using restricted cubic splines with default knot 3 locations. The nonlinear interaction between age and cholesterol is a restricted one such that terms that are nonlinear in both predictors are excluded. This is to save degrees of freedom. The code below also fits the base model containing only age and sex.
3 Knots are locations of shape changes, or more specifically, unique places where the third derivative (jolt) changes. The function and first two derivatives are allowed to change at all points. Knots are locations in the covariate space where cubic polynomials are joined together.
Estimated log odds of the risk of significant CAD is plotted against cholesterol for ages 40 and 70 years for males. One can readily see that the diagnostic value of cholesterol is greater for younger patients, and there is some evidence that very low total cholesterol is risky at age 70.
Logistic Regression Model
lrm(formula = sigdz ~ rcs(age, 4) * sex, data = acath)
| Model Likelihood Ratio Test |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 2258 | LR χ2 489.51 | R2 0.270 | C 0.770 |
| 0 768 | d.f. 7 | R27,2258 0.192 | Dxy 0.539 |
| 1 1490 | Pr(>χ2) <0.0001 | R27,1520.4 0.272 | γ 0.546 |
| max |∂log L/∂β| 1×10-7 | Brier 0.177 | τa 0.242 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| Intercept | -3.9266 | 0.8405 | -4.67 | <0.0001 |
| age | 0.1130 | 0.0213 | 5.30 | <0.0001 |
| age' | -0.0761 | 0.0658 | -1.16 | 0.2477 |
| age'' | 0.1890 | 0.2856 | 0.66 | 0.5082 |
| sex=female | 2.2574 | 1.5121 | 1.49 | 0.1355 |
| age × sex=female | -0.0930 | 0.0378 | -2.46 | 0.0138 |
| age' × sex=female | 0.0629 | 0.1073 | 0.59 | 0.5577 |
| age'' × sex=female | 0.0905 | 0.4412 | 0.21 | 0.8375 |
Logistic Regression Model
lrm(formula = sigdz ~ rcs(age, 4) * sex + rcs(choleste, 4) +
rcs(age, 4) %ia% rcs(choleste, 4), data = acath, x = TRUE,
y = TRUE)
| Model Likelihood Ratio Test |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 2258 | LR χ2 596.99 | R2 0.322 | C 0.795 |
| 0 768 | d.f. 15 | R215,2258 0.227 | Dxy 0.590 |
| 1 1490 | Pr(>χ2) <0.0001 | R215,1520.4 0.318 | γ 0.590 |
| max |∂log L/∂β| 4×10-5 | Brier 0.167 | τa 0.265 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| Intercept | -7.3635 | 4.9896 | -1.48 | 0.1400 |
| age | 0.1688 | 0.1113 | 1.52 | 0.1292 |
| age' | 0.0364 | 0.2516 | 0.14 | 0.8850 |
| age'' | 0.0410 | 1.0461 | 0.04 | 0.9687 |
| sex=female | 3.0665 | 1.6093 | 1.91 | 0.0567 |
| choleste | 0.0145 | 0.0256 | 0.57 | 0.5709 |
| choleste' | 0.0316 | 0.0889 | 0.36 | 0.7226 |
| choleste'' | -0.1417 | 0.2811 | -0.50 | 0.6142 |
| age × choleste | -0.0003 | 0.0006 | -0.51 | 0.6072 |
| age × choleste' | 0.0002 | 0.0017 | 0.12 | 0.9016 |
| age × choleste'' | 0.0005 | 0.0055 | 0.09 | 0.9296 |
| age' × choleste | -0.0004 | 0.0011 | -0.40 | 0.6866 |
| age'' × choleste | 0.0004 | 0.0046 | 0.09 | 0.9301 |
| age × sex=female | -0.1134 | 0.0402 | -2.82 | 0.0048 |
| age' × sex=female | 0.0687 | 0.1140 | 0.60 | 0.5468 |
| age'' × sex=female | 0.1509 | 0.4678 | 0.32 | 0.7471 |
The most basic display of added value is back-to-back high-resolution histograms of pre- and post-test predicted risks. When the new markers add clinically important predictive information, the histogram widens.

Another good way to visualize the diagnostic yield of cholesterol is to plot estimated post vs. pre-test probability of CAD. We use quantile regression to estimate the 0.1 and 0.9 quantiles of post-test risk as a function of pre-test risk. This allows one to readily see the typical changes in a pre-test probability once cholesterol is known.
plot(pre, post, xlab='Pre-Test Probability (age + sex)',
ylab='Post-Test Probability\n(age + sex + cholesterol)', pch=46)
abline(a=0, b=1, col=gray(.8))
lo <- Rq(post ~ rcs(pre, 7), tau=0.1) # 0.1 quantile
hi <- Rq(post ~ rcs(pre, 7), tau=0.9) # 0.9 quantile
at <- seq(0, 1, length=200)
lines(at, Predict(lo, pre=at)$yhat, col='red', lwd=1.5)
lines(at, Predict(hi, pre=at)$yhat, col='red', lwd=1.5)
abline(v=.5, col='red')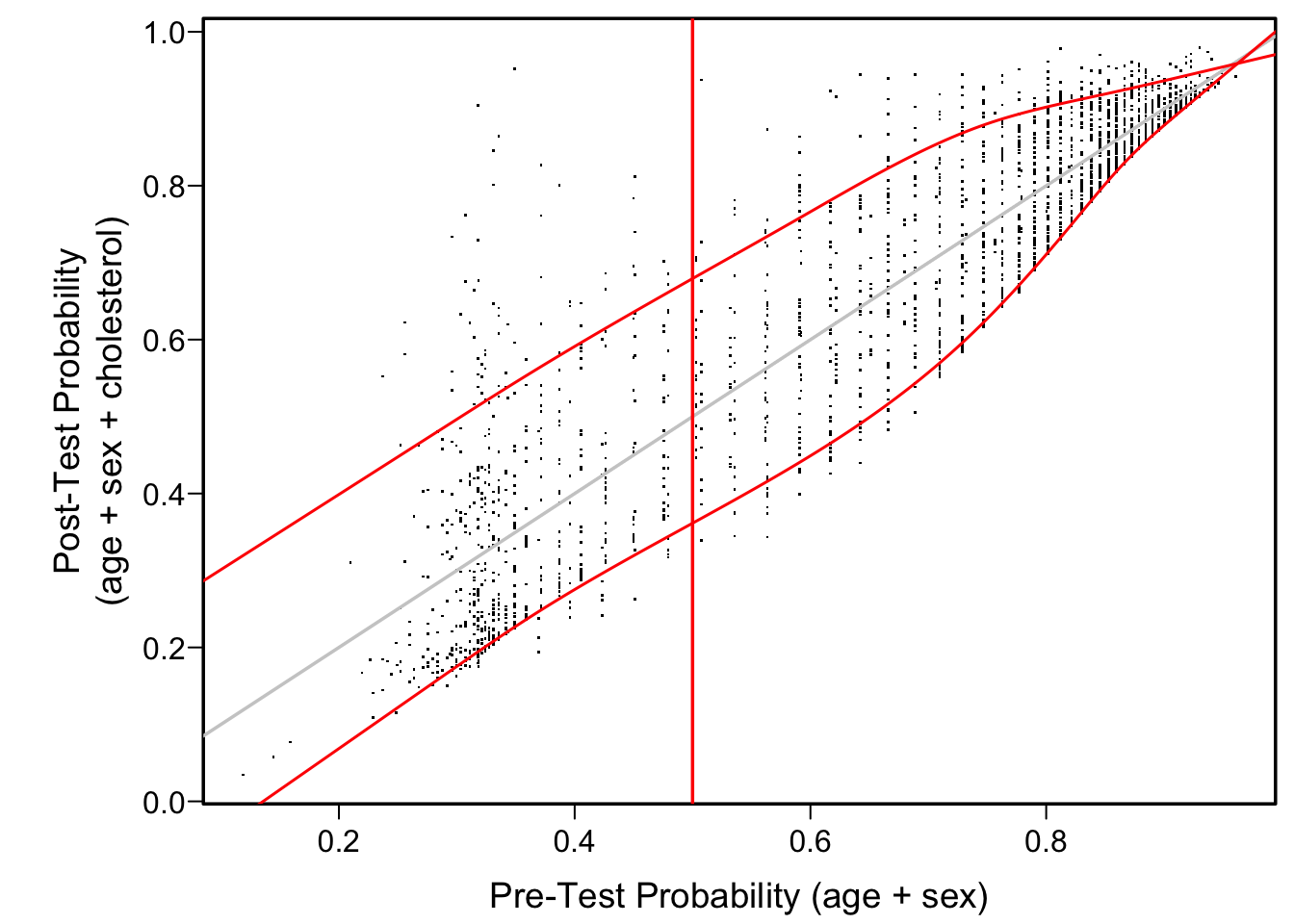
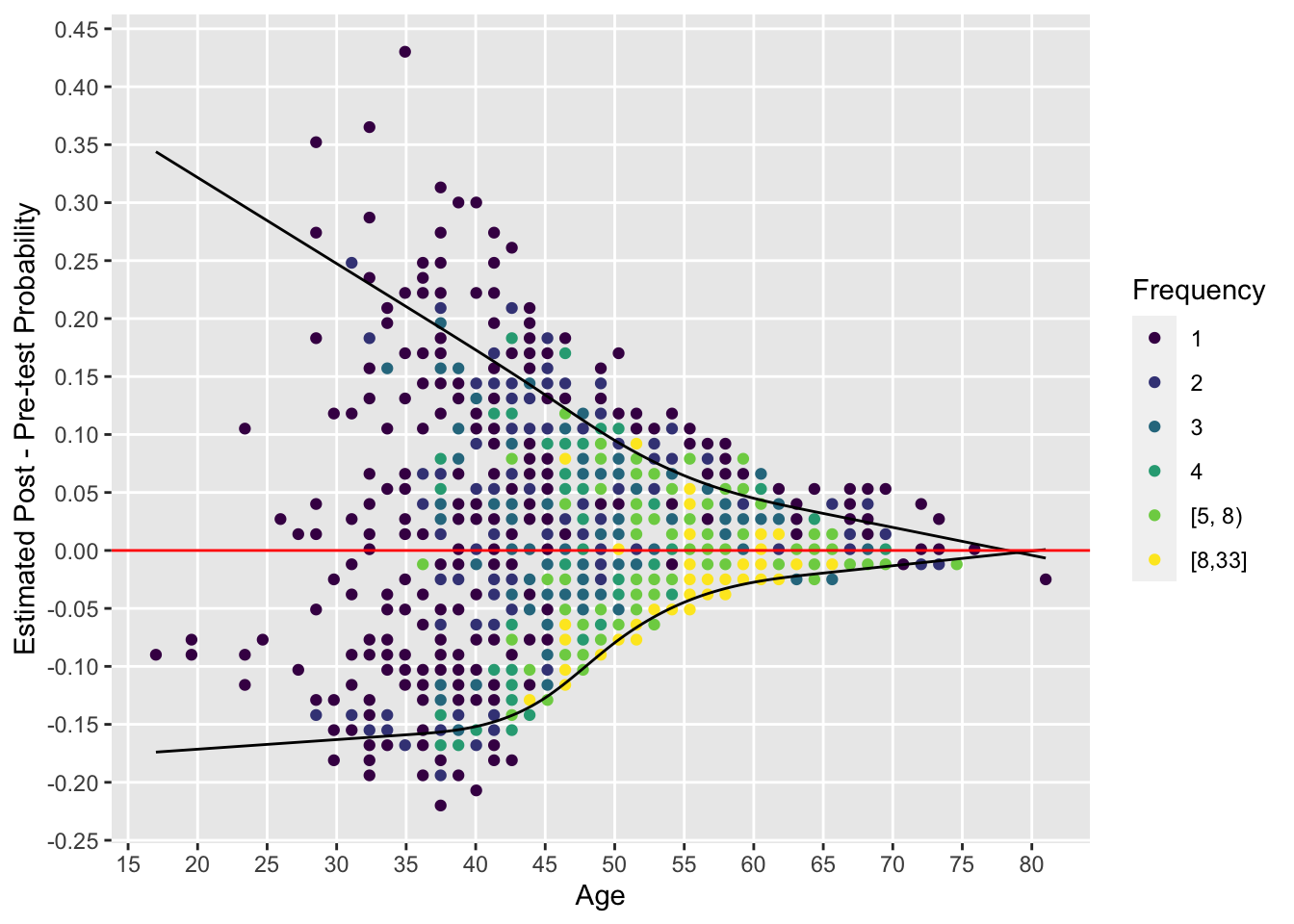
By plotting the pre-post risk difference vs. age we can easily see the dependence on age of the added value of cholesterol. We show the data for males.
d <- cbind(acath, pre=pre, post=post)
with(subset(d, sex == 'male'),
{
lo <- Rq(post - pre ~ rcs(age, 5), tau=0.1)
hi <- Rq(post - pre ~ rcs(age, 5), tau=0.9)
at <- seq(min(age), max(age), length=200)
w <- data.frame(age=at, lo=Predict(lo, age=at)$yhat,
hi=Predict(hi, age=at)$yhat)
ggfreqScatter(age, post - pre,
xlab='Age', ylab='Estimated Post - Pre-test Probability') +
geom_line(aes(x=age, y=lo), data=w, inherit.aes=FALSE) +
geom_line(aes(x=age, y=hi), data=w, inherit.aes=FALSE) +
geom_hline(aes(yintercept=0), col='red')
})
The gold standard LR test for added value of cholesterol is obtained by comparing log likelihoods of the pre and post-test models. Cholesterol has a total of 8 parameters; 5 for interacting with the spline function of age and 3 for its main effect4. Before getting the 8 d.f. LR test, let’s also get the LR test for interaction between cholesterol and age.
4 The LR test could have easily tested multiple new biomarkers simultaneously.
Model 1: sigdz ~ rcs(age, 4) * sex + rcs(choleste, 4)
Model 2: sigdz ~ rcs(age, 4) * sex + rcs(choleste, 4) + rcs(age, 4) %ia%
rcs(choleste, 4)
L.R. Chisq d.f. P
11.19828202 5.00000000 0.04758732
Model 1: sigdz ~ rcs(age, 4) * sex
Model 2: sigdz ~ rcs(age, 4) * sex + rcs(choleste, 4) + rcs(age, 4) %ia%
rcs(choleste, 4)
L.R. Chisq d.f. P
107.4788 8.0000 0.0000 From the last test there is very strong evidence that cholesterol adds diagnostic value. The question is to what extent. So we turn to the various indexes discussed earlier—indexes that are sample-size independent, unlike the LR \(\chi^2\) statistic that doubles when the sample size doubles, all else being equal. As with the graphical summaries above, our indexes require no binning of data and fully allow for cholesterol to have varying importance as a function of age.
The detailed statistics that were listed for the pre- and post-test models above provide the LR \(\chi^2\), Nagelkerke pseudo \(R^2\), three \(g\) indexes (log odds ratio scale, odds ratio scale, and risk scale), Brier score, \(c\)-index, Somers’ \(D_{xy}\), Goodman-Kruskal \(\gamma\), and Kendall’s \(\tau_a\), the latter three being rank correlations between predicted disease risk and actual disease presence. \(D_{xy}\) is connected to \(c\) by \(D_{xy} = 2 (c - \frac{1}{2})\).
Now consider measures of explained variation in disease status, and relative explained variation (REV). Recall that pre- and post-test predicted risks are stored in the variables pre and post, respectively. To get bootstrap confidence intervals for the new REV measure we bootstrap the model.
b <- bootcov(g, B=300)
r <- function(x) round(x, 2)
s <- function(x) round(x, 3)
lra <- f$stats['Model L.R.']
lrb <- g$stats['Model L.R.']
ra <- f$stats['R2']
rb <- g$stats['R2']
br2 <- function(p) var(p) / (var(p) + sum(p * (1 - p)) / length(p))
# Compute the new measure with 0.95 CIs
rv <- rexVar(b, data=acath)
plot(rv, margin=TRUE)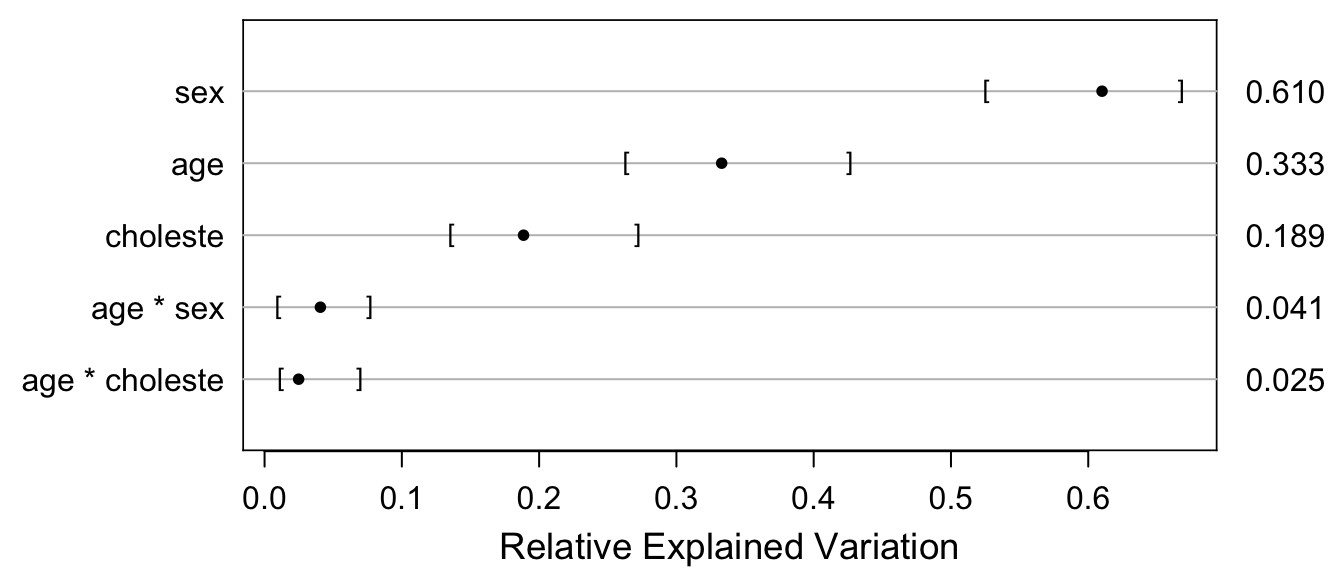
In the table below, “Fraction of new information” is the proportion of total predictive information in age, sex, and cholesterol that was added by cholesterol (main effect + age interaction effect). “Fraction explained risk” is the \(R^2\) measure explicitly for binary Y, i.e., the ratio of the variance of predicted risk to the sum of the variance of predicted risk and the average risk times (1 - risk), computed by the br2 function above. rexVar is from the rexVar function, i.e., is partial \(R^2\) from a bridge linear model (the raw output of rexVar is in row p below).
| Index | Value | Formula | |
|---|---|---|---|
| a | Pre-test LR \(\chi^2\) | 489.51 | |
| b | Post-test LR \(\chi^2\) | 596.99 | |
| c | Adequacy of base model | 0.82 | a/b |
| d | Fraction of new information from cholesterol | 0.18 | 1-c |
| e | Pre-test Nagelkerke pseudo \(R^2\) | 0.27 | |
| f | Post-test Nagelkerke pseudo \(R^2\) | 0.32 | |
| g | Variance of pre-test risk | 0.047 | |
| h | Variance of post-test risk | 0.057 | |
| i | Relative explained variation | 0.83 | g/h |
| j | Fraction of new information | 0.17 | 1-i |
| k | Pre-test fraction explained risk | 0.21 | |
| l | Post-test fraction explained risk | 0.25 | |
| m | Relative explained variation | 0.83 | k/l |
| n | Fraction of new information | 0.17 | 1-m |
| o | rexVar |
0.81 | |
| p | Fraction of new information | 0.19 | 1-o |
By the various indexes in the above table, the fraction of total diagnostic information that was due to the “new” test (cholesterol) ranges from 0.16 to 0.19. My favorite measure for assessing the fraction of diagnostic information that is new information from cholesterol is given by row j, i.e., one minus the ratio of the variance of pre-test probability of disease \(\hat{P}\) to the variance of post-test \(\hat{P}\). This is related to one of the most useful displays one can make: high-resolution histograms of pre- and post-test probabilities, where the emphasis is on the width of the distributions. More discriminating models provide a greater variety of predictions, subject to assuming the model is well-calibrated. See above for histograms for pre- and post-test predicted risks. Row p is also preferred because of its generality, and its provision of confidence intervals prevents overconfidence in our information quantification.
The diagnostic yield of cholesterol is age- and sex-dependent. Measuring cholesterol seldom allows one to rule in or rule out coronary disease with certainty. It adds a fraction of 0.17 of new diagnostic information to age and sex.
The methods described here have wide applicability to diagnostic and prognostic research. One area in particular is ripe for applying the methods: genetics. Genetic markers have been touted as being valuable for diagnosis and prognosis. It would be worthwhile to quantify the added value of genetic markers using one of the above indexes, along with the graphics displaying diagnostic or prognostic yield for individual subjects.
See Fronczek et al. (2021) for an application of added relative information.
Go here to comment, critique, discuss, or put questions about this article. That link also contains an archive of comments previously entered directly on the old blog site.
---
title: Statistically Efficient Ways to Quantify Added Predictive Value of New Measurements
author:
- name: Frank Harrell
url: https://hbiostat.org
affiliation: Department of Biostatistics<br>Vanderbilt University School of Medicine
date: 2018-10-17
modified: 2023-09-24
categories: [prediction, sample-size, validation, accuracy-score, biomarker, diagnosis, medicine, reporting, 2018]
slug: addvalue
description: "Researchers have used contorted, inefficient, and arbitrary analyses to demonstrated added value in biomarkers, genes, and new lab measurements. Traditional statistical measures have always been up to the task, and are more powerful and more flexible. It's time to revisit them, and to add a few slight twists to make them more helpful."
bibliography: /Users/harrelfe/web/bib/harrelfe.bib
---
```{r setup, echo=FALSE}
require(Hmisc)
require(ggplot2)
knitrSet(lang='quarto')
```
::: {.quoteit}
When the outcome variable Y is continuous, there are only three measures of added value that are commonly used: increase in $R^2$, decrease in mean squared prediction error, and decrease in mean absolute prediction error. Why have so many measures been invented when Y is binary or censored?
:::
# Introduction
A recurring topic in clinical and translational research is the assessment of new information provided by molecular, physiologic, imaging, and other biomarkers. The notion of added value is in the predictive sense, either when diagnosing a hidden disease, e.g., predicting current status using a binary or ordinal logistic model, or when predicting future events, e.g., using a time-to-event statistical model to predict future disease occurrence, recurrence of disease, or occurrence of a clinical event such as death or stroke. [[Comments](https://hbiostat.org/comment.html)]{.aside}
Before getting into purely analytical issues, note that there are many study design issues. One of the most common mistakes, sometimes intentional, is to fail to collect variables that are available in medical practice to put into the base model. This leads to inadequate adjustment for prior information, setting the bar too low when measuring added value of new information. Other common mistakes are categorizing some of the adjustment variables, resulting in residual confounding and failure to adjust for the real background variables, and categorizing new continuous measurements, resulting in understatement of their added value. Without knowing it, many translational researchers, by dichotomizing new biomarkers, are requiring additional biomarkers to be measured to make up for the lost information in dichotomized markers.
# How Did We Get Here
Statisticians have no better sense of history than other scientists. In the quest for publishing new ideas, measures of added value are constantly being invented by statisticians, without asking whether older methods already solve the problem at hand. Some of the examples of measures that are commonly used but are not needed in this setting are the $c$-index (@har82; area under the ROC curve if the outcome is binary), and [IDI and NRI](https://onlinelibrary.wiley.com/toc/10970258/27/2). They are not needed because measures based on standard regression methods are not only adequate to the task, but are more powerful and **more flexible and insightful**, especially when interactions are involved. Especially problematic are measures such as the categorical version of NRI (net reclassification improvement) which not only requires arbitrary categorization of risk estimates but then goes on to use inefficient binary summaries from them. Pencina (personal communication) has regretted including statistical tests for these measures in his highly-cited paper, as these tests have nowhere near the power of the gold-standard likelihood ratio test.
Comparing two c-indexes (one from the base model and one from the larger model containing the new biomarkers) is a low-power procedure. This is because the c-index is a rank measure (the concordance probability from the Wilcoxon test or Somers' $D_{xy}$ rank correlation) that does not sufficiently reward extreme predictions that are correct^[The Wilcoxon, Spearman, and other rank tests are very powerful for testing for existence of an association, but not for assessing *differences* in the strength of association.]. And taking the difference between two c-indexes corresponds to taking the difference in two Wilcoxon statistics, which is never done. Instead, a head-to-head comparison is demanded. This can be done by using a different U-statistic based on all possible pairs of observations and counting the fraction of pairs for which one model is "more concordant" with the outcome than the other model. This respects pairings of pairings, and is implemented in the R `Hmisc` package `rcorrp.cens` function. Still, this is not as powerful as the likelihood ratio $\chi^2$ test.
Worse than any of these problems is the continued use of [discontinuous improper accuracy scoring rules](/post/class-damage) such as sensitivity, specificity, precision, and recall.
# Key Measures
There are three gold standards, and statisticians have too often tried to forget them in the search for novelty:
* frequentist: log-likelihood, including the likelihood ratio $\chi^2$ test (LR) and AIC
* Bayesian: log-likelihood + log prior, including various Bayesian information criteria
* explained variation in Y
Methods based on one of these gold standards are simpler, more powerful, and allow for greater complexity. The best example of handling complexity will be demonstrated in the case study below, in which the new marker interacts with a standard variable (there, age) when predicting disease probability.
In the binary outcome (Y) case, there are two commonly used proper accuracy scores: the logarithmic accuracy score (a per-observation log-likelihood), and the quadratic accracy score (Brier score; mean squared error). The log-likelihood can be turned into a 0-1 pseudo $R^2$ measure: $1 - \exp(-\text{LR} / n)$. The only thing going against pseudo $R^2$ is the difficulty in interpreting its absolute value. But it is excellent for comparing two or more models, even though examining increases in LR is better.
Explained outcome variation is another key type of measure. In the linear model, the traditional $R^2$ is often used. This is SSR / SST where SSR is the sum of squares due to regression (the sum of squares of differences between predicted values and the mean predicted value), and SST is the sum of squares total, which is n-1 times the variance of Y. $R^2$ may also be written as SSR / (SSR + SSE) where SSE is the sum of squared residuals. In the linear model, $R^2$ and the log-likelihood are measuring the same thing since LR = $-n \log(1 - R^{2})$.
We can re-express $R^2$ as $\frac{\text{var}(\hat{Y})}{\text{var}(Y)}$ where $\hat{Y} = X \hat{\beta}$ is the linear predictor (predicted mean, for the linear model).
$R^2$ can equivalently be written as the ratio of the explained variance to the sum of explained and unexplained variance. The unexplained variance is the variance of the residuals in the linear model. For a probability model, the natural way to express the proportion of explained variance is through the predicted probabilities that Y=1, denoted by $\hat{P}$. The $R^2$ measure for a binary Y model is then $$\frac{\text{var}(\hat{P})}{\text{var}(\hat{P}) + \sum_{i}^{n} \hat{P}_{i} (1 - \hat{P}_{i}) / n}$$
where $\text{var}(\hat{P})$ is the sample variance of the $n$ $\hat{P}_{i}$.^[@sch03pre is an excellent paper advocating for measures based on absolute rather than squared differences.]
@ken88mea have extended the idea of the fraction of explained variation in the outcome to various nonlinear models including those used in survival analysis. The SST or var(Y) is distribution-specific. The beauty of this approach is its focus on the variance of $\hat{Y}$, which is independent of the prevalence of Y=1 in the binary case and of the amount of censoring in time-to-event analysis. See also @cho12simII and @cho12simI.
A different type of key measure will also be exemplified in the case study: differences in predicted values between the base model and the expanded model.
## Relative Explained Variation
Relative explained variation is a simple concept that has the extra advantage of being completely free of the distribution of Y and the customized error variance or SST necessary for computing the proportion of explained variance for distributions other than the normal. For a linear model relative explained variation is the ratio of the $R^2$ for the base model to the larger $R^2$ for the combined model that contains also the new markers being tested. And since for $R^{2} \leq 0.25$, $-n \log(1 - R^{2})$ is approximately $n R^{2}$, the relative variation explained by the base variables is approximately equal to the _adequacy index_ discussed in the maximum likelihood estimation chapter of [Regression Modeling Strategies](http://hbiostat.org/rms) (@rms2): $$\text{Adequacy index} = \text{LR}_{A} / \text{LR}_{AB}$$ where the base model is denoted by A, the added predictors (e.g., biomarkers) are denoted by B, AB represents the combined model with A and B as predictors, and LR is defined above. Here adequacy refers to the adequacy of the model that ignores the new predictors.
Whether using the adequacy index or relative variation explained, one minus such an index is the fraction of new information provided by predictors in B. It is the proportion of explainable variation that is explained by B.
To emphasize the simplicity of relative explained variation, it is just the ratio of variances of predicted values. And other statistical indexes may be computed from the predicted values, such as the mean absolute difference from the mean predicted value, and the $g$ index described in _Regression Modeling Strategies_. The latter is the mean absolute difference between any two predicted values. But it is possible for the $g$ index for AB to be smaller than that for model A.
A general-purpose way to compute relative explained variable for virtually any regression model is to use the linear model as a bridge to the current model. The linear model is fitted to the linear predictor (here the predicted log odds) developed from the model of interest. The linear model will exactly reproduce our model, with $R^{2}=1.0$. Use the ordinary partial $R^2$ from the linear model fit to estimate relative explained variation in the original model on the linear predictor scale. The R `rms` package `rexVar` function does these calculations, and if the model is a Bayesian model or was bootstrapped with the R `rms` `bootcov` function with `coef.reps=TRUE` uncertainty intervals for relative explained variation are also computed. [`rexVar` is available in `rms` 6.8-0]{.aside}
[Here](https://hbiostat.org/rmsc/validate#sec-val-rev) is a full example for the new measure.
# Case Study: Quantifying Diagnostic Information
Consider a series of patients from the Duke Cardiovascular Disease Databank. These patients were referred to Duke University Medical Center for chest pain and underwent cardiac catheterization during which a dye is injected and a coronary angiography is used to view blockages of coronary arteries. Significant coronary artery disease is here defined as a blockage of at least 75% by vessel diameter, in at least one major coronary artery. Here we consider total cholesterol as if it were a new diagnostic marker, and we wish to quantify the new diagnostic information provided by cholesterol. The base model is oversimplified for purposes of illustration. It contains only the powerful variables age and sex. In practice it should contain in addition to age and sex all relevant easily available baseline variables, such as pain characteristics, blood pressure, smoking history, etc. From previous analysis, a nonlinear interaction was demonstrated between age and sex and between age and cholesterol. The former is related to women "catching up" with men with respect to cardiovascular risk, after menopause. The latter interaction captures the fact that high cholesterol is not as dangerous for older patients and the possibility that very low cholesterol is actually harmful for them.
The dataset is available from the Vanderbilt Department of Biostatistics wiki, and includes 2258 patients with all variables measured. It may be automatically downloaded using the R `Hmisc getHdata` function. The dataset is also analyzed in the [BBR diagnosis chapter](http://hbiostat.org/bbr/dx.html) and [here](http://hbiostat.org/talks/memtab18.pdf). The latter link contains more analyses that compare pre- and post-test probabilities.
## Development of Binary Logistic Model
We first fit a binary logistic regression model with interactions, modeling age and cholesterol in a smooth nonlinear fashion using restricted cubic splines with default knot ^[Knots are locations of shape changes, or more specifically, unique places where the third derivative (jolt) changes. The function and first two derivatives are allowed to change at all points. Knots are locations in the covariate space where cubic polynomials are joined together.] locations. The nonlinear interaction between age and cholesterol is a restricted one such that terms that are nonlinear in both predictors are excluded. This is to save degrees of freedom. The code below also fits the base model containing only age and sex.
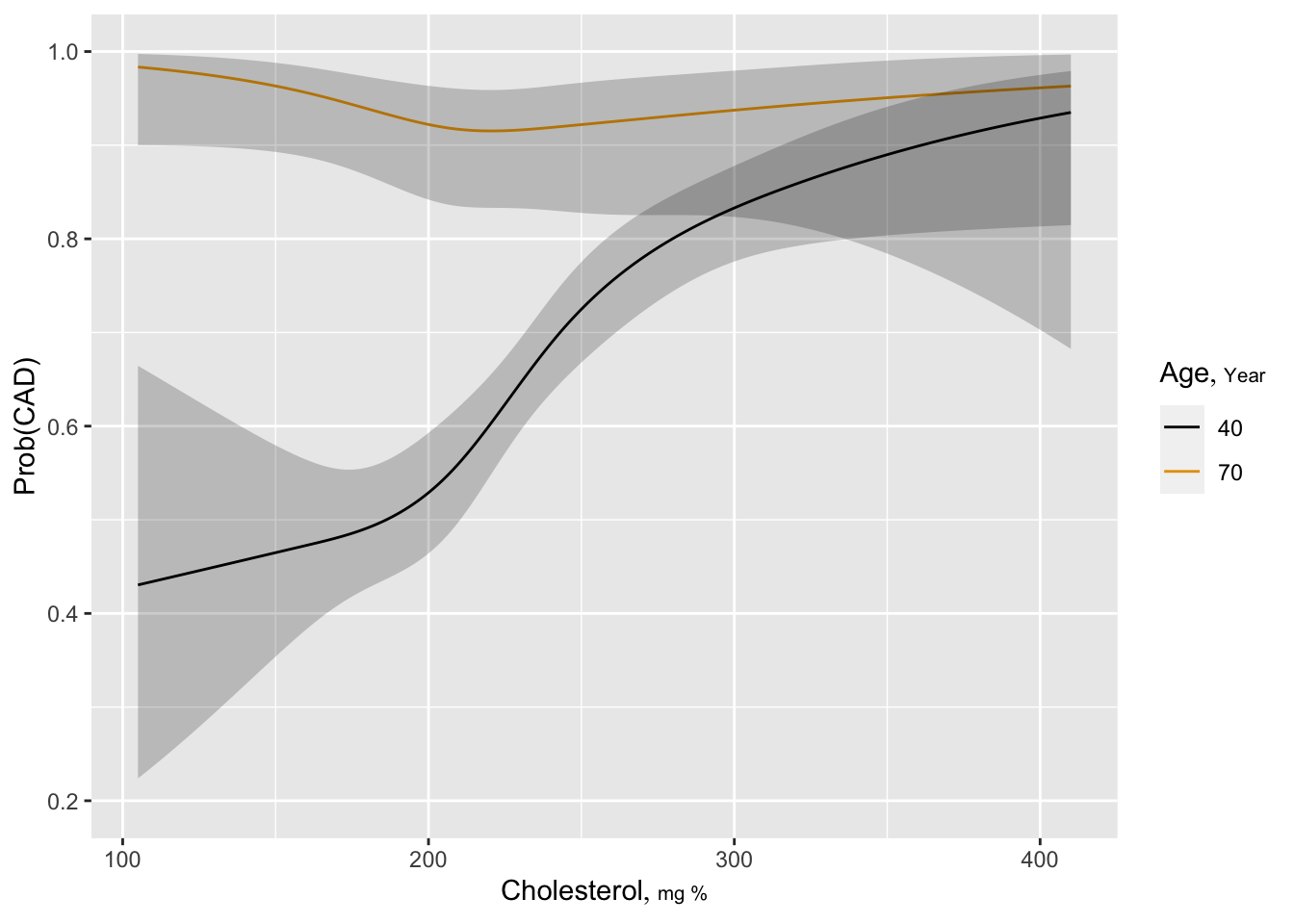
Estimated log odds of the risk of significant CAD is plotted against cholesterol for ages 40 and 70 years for males. One can readily see that the diagnostic value of cholesterol is greater for younger patients, and there is some evidence that very low total cholesterol is risky at age 70.
```{r fit,results='asis'}
require(rms)
require(ggplot2)
options(prType='html')
getHdata(acath)
acath <- subset(acath, !is.na(choleste))
acath$sex <- factor(acath$sex, 0:1, c('male', 'female'))
dd <- datadist(acath); options(datadist='dd')
f <- lrm(sigdz ~ rcs(age,4) * sex, data=acath)
f
pre <- predict(f, type='fitted') # pre-test probability
g <- lrm(sigdz ~ rcs(age,4) * sex + rcs(choleste,4) + rcs(age,4) %ia%
rcs(choleste,4), data=acath, x=TRUE, y=TRUE) # x,y for bootcov
g
post <- predict(g, type='fitted') # post-test probability
ageg <- c(40, 70) # test=cholesterol
psig <- Predict(g, choleste, age=ageg, sex='male', fun=plogis)
ggplot(psig, adj.subtitle=FALSE, ylab='Prob(CAD)')
```
## Visualizing Information Provided by Cholesterol By Analyzing Pre- and Post-test Probabilities
The most basic display of added value is back-to-back high-resolution histograms of pre- and post-test predicted risks. When the new markers add clinically important predictive information, the histogram widens.
```{r hist}
par(mgp=c(4,1,0), mar=c(6,5,2,2))
xlab <- c(paste0('Pre-test\nvariance=', round(var(pre), 3)),
paste0('Post-test\nvariance=',round(var(post), 3)))
histbackback(pre, post, brks=seq(0.01, 0.99, by=0.01), xlab=xlab, ylab='Prob(CAD)')
```
Another good way to visualize the diagnostic yield of cholesterol is to plot estimated post vs. pre-test probability of CAD. We use quantile regression to estimate the 0.1 and 0.9 quantiles of post-test risk as a function of pre-test risk. This allows one to readily see the typical changes in a pre-test probability once cholesterol is known.
```{r prepost}
plot(pre, post, xlab='Pre-Test Probability (age + sex)',
ylab='Post-Test Probability\n(age + sex + cholesterol)', pch=46)
abline(a=0, b=1, col=gray(.8))
lo <- Rq(post ~ rcs(pre, 7), tau=0.1) # 0.1 quantile
hi <- Rq(post ~ rcs(pre, 7), tau=0.9) # 0.9 quantile
at <- seq(0, 1, length=200)
lines(at, Predict(lo, pre=at)$yhat, col='red', lwd=1.5)
lines(at, Predict(hi, pre=at)$yhat, col='red', lwd=1.5)
abline(v=.5, col='red')
```
By plotting the pre-post risk difference vs. age we can easily see the dependence on age of the added value of cholesterol. We show the data for males.
```{r vsage}
d <- cbind(acath, pre=pre, post=post)
with(subset(d, sex == 'male'),
{
lo <- Rq(post - pre ~ rcs(age, 5), tau=0.1)
hi <- Rq(post - pre ~ rcs(age, 5), tau=0.9)
at <- seq(min(age), max(age), length=200)
w <- data.frame(age=at, lo=Predict(lo, age=at)$yhat,
hi=Predict(hi, age=at)$yhat)
ggfreqScatter(age, post - pre,
xlab='Age', ylab='Estimated Post - Pre-test Probability') +
geom_line(aes(x=age, y=lo), data=w, inherit.aes=FALSE) +
geom_line(aes(x=age, y=hi), data=w, inherit.aes=FALSE) +
geom_hline(aes(yintercept=0), col='red')
})
```
## Statistical Indexes for Added Value of Cholesterol
The gold standard LR test for added value of cholesterol is obtained by comparing log likelihoods of the pre and post-test models. Cholesterol has a total of 8 parameters; 5 for interacting with the spline function of age and 3 for its main effect^[The LR test could have easily tested multiple new biomarkers simultaneously.]. Before getting the 8 d.f. LR test, let's also get the LR test for interaction between cholesterol and age.
```{r lr}
h <- lrm(sigdz ~ rcs(age,4)*sex + rcs(choleste,4), data=acath)
lrtest(h, g) # test interaction
lrtest(f, g) # test cholesterol as main or interacting effect
# These can be automatically computed using
# anova(g, test='LR')
```
From the last test there is very strong evidence that cholesterol adds diagnostic value. The question is to what extent. So we turn to the various indexes discussed earlier---indexes that are sample-size independent, unlike the LR $\chi^2$ statistic that doubles when the sample size doubles, all else being equal.
As with the graphical summaries above, our indexes require no binning of data and fully allow for cholesterol to have varying importance as a function of age.
The detailed statistics that were listed for the pre- and post-test models above provide the LR $\chi^2$, Nagelkerke pseudo $R^2$, three $g$ indexes (log odds ratio scale, odds ratio scale, and risk scale), Brier score, $c$-index, Somers' $D_{xy}$, Goodman-Kruskal $\gamma$, and Kendall's $\tau_a$, the latter three being rank correlations between predicted disease risk and actual disease presence. $D_{xy}$ is connected to $c$ by $D_{xy} = 2 (c - \frac{1}{2})$.
### New Old Measures
Now consider measures of explained variation in disease status, and relative explained variation (REV). Recall that pre- and post-test predicted risks are stored in the variables `pre` and `post`, respectively. To get bootstrap confidence intervals for the new REV measure we bootstrap the model.
```{r comp}
#| fig-height: 3
b <- bootcov(g, B=300)
r <- function(x) round(x, 2)
s <- function(x) round(x, 3)
lra <- f$stats['Model L.R.']
lrb <- g$stats['Model L.R.']
ra <- f$stats['R2']
rb <- g$stats['R2']
br2 <- function(p) var(p) / (var(p) + sum(p * (1 - p)) / length(p))
# Compute the new measure with 0.95 CIs
rv <- rexVar(b, data=acath)
plot(rv, margin=TRUE)
```
In the table below, "Fraction of new information" is the proportion of total predictive information in age, sex, and cholesterol that was added by cholesterol (main effect + age interaction effect). "Fraction explained risk" is the $R^2$ measure explicitly for binary Y, i.e., the ratio of the variance of predicted risk to the sum of the variance of predicted risk and the average risk times (1 - risk), computed by the `br2` function above. `rexVar` is from the `rexVar` function, i.e., is partial $R^2$ from a bridge linear model (the raw output of `rexVar` is in row p below).
| | Index | Value | Formula |
|-|----------------------------------|-------------------------------|---------|
|a| Pre-test LR $\chi^2$ | `r r(lra)` | |
|b| Post-test LR $\chi^2$ | `r r(lrb)` | |
|c| Adequacy of base model | `r r(lra/lrb)` | a/b |
|d| Fraction of new information from cholesterol| `r r(1 - lra/lrb)` | 1-c |
|e| Pre-test Nagelkerke pseudo $R^2$ | `r r(ra)` | |
|f| Post-test Nagelkerke pseudo $R^2$| `r r(rb)` | |
|g| Variance of pre-test risk | `r s(var(pre))` | |
|h| Variance of post-test risk | `r s(var(post))` | |
|i| Relative explained variation | `r r(var(pre)/var(post))` | g/h |
|j| Fraction of new information | `r r(1 - var(pre)/var(post))` | 1-i |
|k| Pre-test fraction explained risk | `r r(br2(pre))` | |
|l| Post-test fraction explained risk| `r r(br2(post))` | |
|m| Relative explained variation | `r r(br2(pre)/br2(post))` | k/l |
|n| Fraction of new information | `r r(1 - br2(pre)/br2(post))` | 1-m |
|o| `rexVar` | `r r(1 - rv['choleste', 'REV'])` | |
|p| Fraction of new information | `r r(rv['choleste', 'REV'])` | 1-o |
By the various indexes in the above table, the fraction of total diagnostic information that was due to the "new" test (cholesterol) ranges from 0.16 to 0.19. My favorite measure for assessing the fraction of diagnostic information that is new information from cholesterol is given by row j, i.e., one minus the ratio of the variance of pre-test probability of disease $\hat{P}$ to the variance of post-test $\hat{P}$. This is related to one of the most useful displays one can make: high-resolution histograms of pre- and post-test probabilities, where the emphasis is on the width of the distributions. More discriminating models provide a greater variety of predictions, subject to assuming the model is well-calibrated. See above for histograms for pre- and post-test predicted risks. Row p is also preferred because of its generality, and its provision of confidence intervals prevents overconfidence in our information quantification.
## Analysis Conclusions
The diagnostic yield of cholesterol is age- and sex-dependent. Measuring cholesterol seldom allows one to rule in or rule out coronary disease with certainty. It adds a fraction of 0.17 of new diagnostic information to age and sex.
# Areas of Application
The methods described here have wide applicability to diagnostic and prognostic research. One area in particular is ripe for applying the methods: genetics. Genetic markers have been touted as being valuable for diagnosis and prognosis. It would be worthwhile to quantify the added value of genetic markers using one of the above indexes, along with the graphics displaying diagnostic or prognostic yield for individual subjects.
See @fro21rel for an application of added relative information.
# Discussion
Go [here](https://discourse.datamethods.org/t/statistically-efficient-ways-to-quantify-added-predictive-value-of-new-measurements) to comment, critique, discuss, or put questions about this article. That link also contains an archive of comments previously entered directly on the old blog site.
# References