EHRs and RCTs: Outcome Prediction vs. Optimal Treatment Selection
Background
It is often said that randomized clinical trials (RCTs) are the gold standard for learning about therapeutic effectiveness. This is because the treatment is assigned at random so no variables, measured or unmeasured, will be truly related to treatment assignment. The result is an unbiased estimate of treatment effectiveness. On the other hand, observational data arising from clinical practice has all the biases of physicians and patients in who gets which treatment. Some treatments are indicated for certain types of patients; some are reserved for very sick ones. The fact is that the selection of treatment is often chosen on the basis of patient characteristics that influence patient outcome, some of which may be unrecorded. When the outcomes of different groups of patients receiving different treatments are compared, without adjustment for patient characteristics related to treatment selection and outcome, the result is a bias called confounding by indication.
To set the stage for our discussion of the challenges caused by confounding by indication, incomplete data, and unreliable data, first consider a nearly ideal observational treatment study then consider an ideal RCT. First, consider a potentially optimal observational cohort design that has some possibility of providing an accurate treatment outcome comparison. Suppose that an investigator has obtained $2M in funding to hire trained research nurses to collect data completely and accurately, and she has gone to the trouble of asking five expert clinicians in the disease/treatment area to each independently list the patient characteristics they perceive are used to select therapies for patients. The result is a list of 18 distinct patient characteristics, for which a data dictionary is written and case report forms are collected. Data collectors are instructed to obtain these 18 variables on every patient with very few exceptions, and other useful variables, especially strong prognostic factors, are collected in addition. Details about treatment are also captured, including the start and ending dates of treatment, doses, and dose schedule. Outcomes are well defined and never missing. The sample size is adequate, and when data collection is complete, analysis of covariance is used to estimate the outcome difference for treatment A vs. treatment B. Then the study PI discovers that there is a strong confounder that none of the five experts thought of, and a sensitivity analysis indicates that the original treatment effect estimate might have been washed away by the additional confounder had it been collected. The study results in no reliable knowledge about the treatments.
The study just described represents a high level of observational study quality, and still needed some luck to be useful. The treatments, entry criteria, and follow-up clock were well defined, and there were almost no missing data. Contrast that with the electronic health record (EHR). If questions of therapeutic efficacy are so difficult to answer with nearly perfect observational data how can they be reliably answered from EHR data alone?
To complete our introduction to the discussion, envision a well-conducted parallel-group RCT with complete follow-up and highly accurate and relevant baseline data capture. Study inclusion criteria allowed for a wide range of age and severity of disease. The endpoint is time until a devastating clinical event. The treatment B:treatment A covariate-adjusted hazard ratio is 0.8 with 0.95 credible interval of [0.65, 0.93]. The authors, avoiding unreliable subgroup analysis, perform a careful but comprehensive assessment of interaction between patient types and treatment effect, finding no evidence for heterogeneity of treatment effect (HTE). The hazard ratio of 0.8 is widely generalizable, even to populations with much different baseline risk. A simple nomogram is drawn to show how to estimate absolute risk reduction by treatment B at 3 years, given a patient’s baseline 3y risk.
Limitations of Electronic Health Record Effectiveness Research
There is an alarming trend in advocates of learning from the EHR saying that statistical inference can be bypassed because (1) large numbers overcome all obstacles, (2) the EHR reflects actual clinical practice and patient populations, and (3) if you can predict outcomes for individual patients you can just find out for which treatment the predicted outcomes are optimal. Advocates of such “logic” often go on to say that RCTs are not helpful because the proportion of patients seen in practice that would qualify for the trial is very small with randomized patients being unrepresentative of the clinical population, because the trial only estimates the average treatment effect, because there must be HTE, and because treatment conditions are unrepresentative. Without HTE, precision medicine would have no basis. But evidence of substantial HTE has yet to be generally established and its existence in particular cases can be an artifact of the outcome scale used for the analysis. See this for more about the first two complaints about RCTs. Regarding (1), researchers too often forget that measurement or sample bias does not diminish no matter how large the sample size. Often, large sample sizes only provide precise estimates of the wrong quantity.
To illustrate this problem, suppose that one is interested in estimating and testing the treatment effect, B-A, of a certain blood pressure lowering medication (drug B) when compared to another drug (A). Assume a relevant subset of the EHR can be extracted in which patients started initial monotherapy at a defined date and systolic blood pressure (SBP) was measured routinely at useful follow-up intervals. Suppose that the standard deviation (SD) of SBP across patients is 8 mmHg regardless of treatment group. Suppose further that minor confounding by indication is present due to the failure to adjust for an unstated patient feature involved in the drug choice, which creates a systematic unidirectional bias of 2 mmHg in estimating the true B-A difference in mean SBP. If the EHR has m patients in each treatment group, the variance of the estimated mean difference is the sum of the variances of the two individual means or 64/m + 64/m = 128/m. But the variance only tells us about how close our sample estimate is to the incorrect value, B-A + 2 mmHg. It is the mean squared error, the variance plus the square of the bias or 128/m + 4, that relates to the probability that the estimate is close to the true treatment effect B-A. As m gets larger, the variance goes to zero indicating a stable estimate has been achieved. But the bias is constant so the mean squared error remains at 4 (root mean squared error = 2 mmHg).
Now consider an RCT that is designed not to estimate the mean SBP for A or the mean SBP for B but, as with all randomized trials, is designed to estimate the B-A difference (treatment effect). If the trial randomized m subjects per treatment group, the variance of the mean difference is 128/m and the mean squared error is also 128/m. The comparison of the square root of mean squared errors for an EHR study and an equal-sized RCT is depicted in the figure below. Here, we have even given the EHR study the benefit of the doubt in assuming that SBP is measured as accurately as would be the case in the RCT. This is unlikely, and so in reality the results presented below are optimistic for the performance of the EHR.
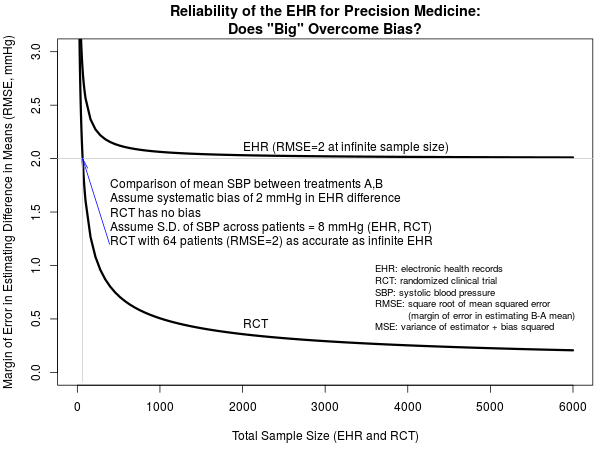
EHR studies have the potential to provide far larger sample sizes than RCTs, but note that an RCT with a total sample size of 64 subjects is as informative as an EHR study with infinitely many patients. Bigger is not better. What if the SBP measurements from the EHR, not collected under any protocol, are less accurate than those collected under the RCT protocol? Let’s exemplify that by setting the SD for SBP to 10 mmHg for the EHR while leaving it as 8 mmHg for the RCT. For very large sample sizes, bias trumps variance so the breakeven point of 64 subjects remains, but for non-large EHRs the increased variability of measured SBPs harms the margin of error of EHR estimate of mean SBP difference.
We have addressed estimation error for the treatment effect, but note that while an EHR-based statistical test for any treatment difference will have excellent power for large n, this comes at the expense of being far from preserving the type I error, which is essentially 1.0 due to the estimation bias causing the two-sample statistical test to be biased.
Interestingly, bias decreases the benefits achieved by larger sample sizes to the extent that, in contrast to an unbiased RCT, the mean squared error for an EHR of size 3000 in our example is nearly identical to what it would be with an infinite sample size. While this disregards the need for larger samples to target multiple treatments or distinct patient populations, it does suggest that overcoming the specific resource-intensive challenges associated with handling huge EHR samples may yield fewer advances in medical treatment than anticipated by some, if the effects of bias are considered.
There is a mantra heard in data science that you just need to “let the data speak.” You can indeed learn much from observational data if quality and completeness of data are high (this is for another discussion; EHRs have major weakness just in these two aspects). But data frequently teach us things that are just plain wrong. This is due to a variety of reasons, including seeing trends and patterns that can be easily explained by pure noise. Moreover, treatment group comparisons in EHRs can reflect both the effects of treatment and the effects of specific prior patient conditions that led to the choice of treatment in the first place - conditions that may not be captured in the EHR. The latter problem is confounding by indication, and this can only be overcome by randomization, strong assumptions, or having high-quality data on all the potential confounders (patient baseline characteristics related to treatment selection and to outcome–rarely if ever possible). Many clinical researchers relying on EHRs do not take the time to even list the relevant patient characteristics before rationalizing that the EHR is adequate. To make matters worse, EHRs frequently do not provide accurate data on when patients started and stopped treatment. Furthermore, the availability of patient outcomes can depend on the very course of treatment and treatment response under study. For example, when a trial protocol is not in place, lab tests are not ordered at pre-specified times but because of a changing patient condition. If EHR cannot provide a reliable estimate of the average treatment effect how could it provide reliable estimates of differential treatment benefit (HTE)?
Regarding the problem with signal vs. noise in “let the data speak”, we envision a clinician watching someone playing a slot machine in Las Vegas. The clinician observes that a small jackpot was hit after 17 pulls of the lever, and now has a model for success: go to a random slot machine with enough money to make 17 pulls. Here the problem is not a biased sample but pure noise.
Observational data, when complete and accurate, can form the basis for accurate predictions. But what are predictions really good for? Generally speaking, predictions can be used to estimate likely patient outcomes given prevailing clinical practice and treatment choices, with typical adherence to treatment. Prediction is good for natural history studies and for counseling patients about their likely outcomes. What is needed for selecting optimum treatments is an answer to the “what if” question: what is the likely outcome of this patient were she given treatment A vs. were she given treatment B? This is inherently a problem of causal inference, which is why such questions are best answered using experimental designs, such as RCTs. When there is evidence that the complete, accurate observational data captured and eliminated confounding by indication, then and only then can observational data be a substitute for RCTs in making smart treatment choices.
Recommended Strategy
What is a good global strategy for making optimum decisions for individual patients? Much more could be said, but for starters consider the following steps:
- Obtain the best covariate-adjusted estimate of relative treatment effect (e.g., odds ratio, hazards ratio) from an RCT. Check whether this estimate is constant or whether it depends on patient characteristics (i.e., whether heterogeneity of treatment effect exists on the relative scale). One possible strategy, using fully specified interaction tests adjusted for all main effects, is in Biostatistics for Biomedical Research.
- Develop a predictive model from complete, accurate observational data, and perform strong interval validation using the bootstrap to verify absolute calibration accuracy. Use this model to handle risk magnification whereby absolute treatment benefits are greater for sicker patients in most cases.
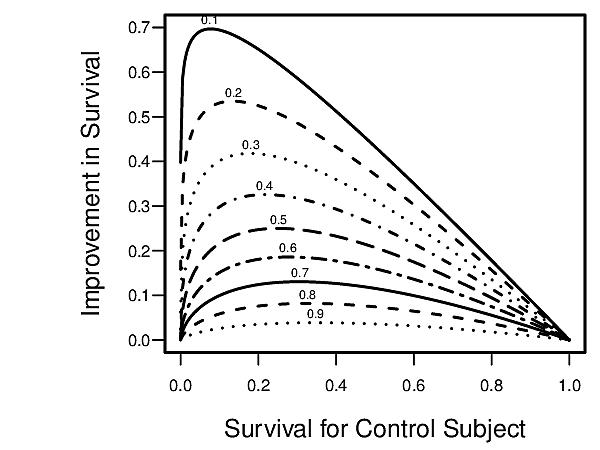
- Apply the relative treatment effects from the RCT, separately for treatment A and treatment B, to the estimated outcome risk from the observational data to obtain estimates of absolute treatment benefit (B vs. A) for the patient. See the first figure below which relates a hazard ratio to absolute improvement in survival probability.
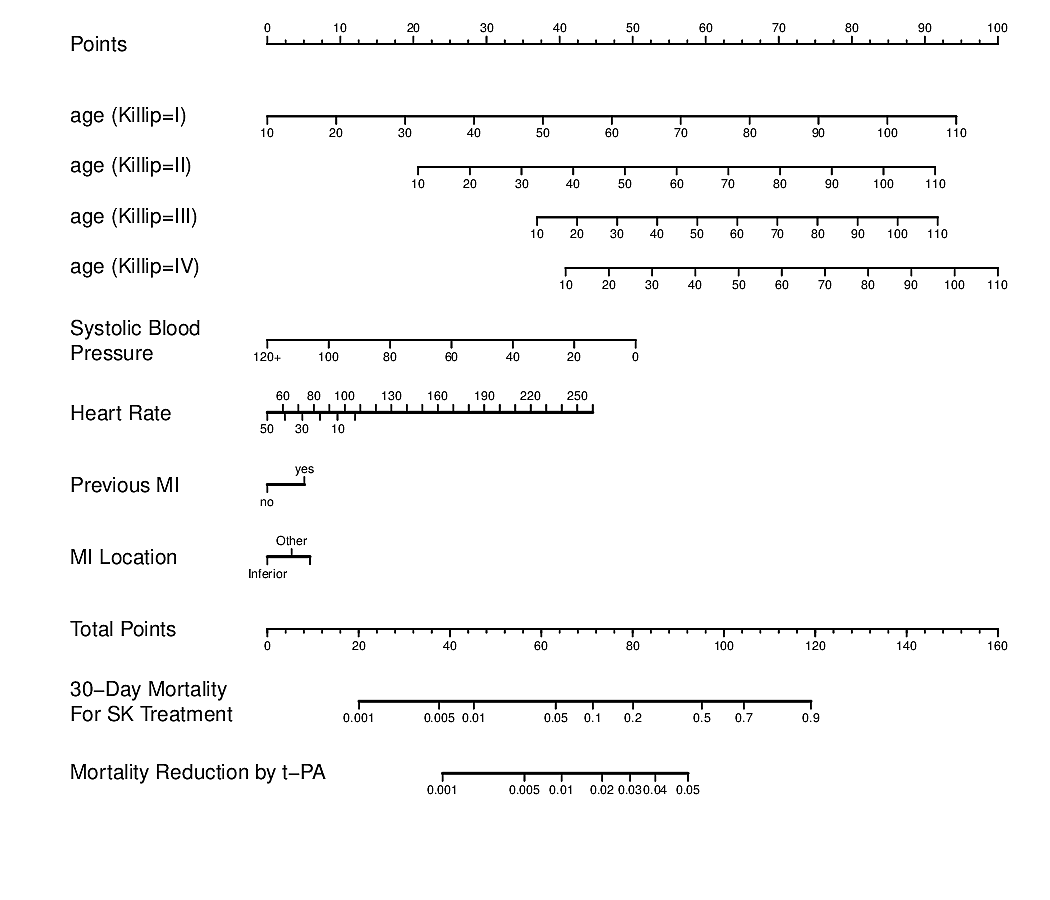
- Develop a nomogram using the RCT data to estimate absolute treatment benefit for an individual patient. See the second figure below whose bottom axis is the difference between two logistic regression models. (Both figures are from BBR)
- For more about such strategies, see Stephen Senn’s presentation.
Further Reading
- Large-scale comparison of causal inference from observational data vs. randomized trials
- Found that estimates from observational data do not accurately capture true effect sizes for advertising interventions
- The magic of randomization versus the myth of real-world evidence by Collins et al
- Unrepresentative big surveys significantly overestimated US vaccine update by VC Bradley et al. “We show how a survey of 250,000 respondents can produce an estimate of the population mean that is no more accurate than an estimate from a simple random sample of size 10.” Paper includes discussion of bias-corrected effective sample size.
- The big data paradox in cliniical practice by Pavlos Msaouel
Discussion Archive (2017)
Qi Tang: I wouldn’t put EHRs against RCTs. Using both for clinical decision making can potential overcome limitations of the two (confounding issues of EHRs and generalization problem of RCTs). It will be great if statisticians can collaborate with data scientists to jointly model them to better understand treatment effect heterogeneities and help physicians to better treat patients.
Frank Harrell: Hi Qi - thanks for the comments. Data science is unlikely to yield a lot of new, validated knowledge about HTE in my humble opinion. The issues are quite nuanced statistically. But I may be proven wrong. But I think you didn’t quite get one of the main points of the post - RCTs are generalizable in what they were intended to estimate - relative efficacy. Observational data (including EHRs but not limited to them) provides information about absolute risk that will allow one to translate relative benefit to absolute benefit. Observational data provides very little information about HTE. If observational data cannot reliably estimate the average treatment effect, it almost surely cannot estimate differential treatment effects (HTE).
FH: With the caveats you listed towards the end I agree. I just see too many observational studies for which investigators try to estimate therapeutic effectiveness where we can’t trust the data, the adequacy of confounder adjustment, and the constitution of the sample. Regarding under-representation of some patient types, I see that sometimes, but lots of RCTs have enough variation in patient characteristics to give us what we need. Thanks very much for the excellent comments.
Ibrahim M Abbass: Great article Frank. As a user of big data in healthcare, I have seen much abuse of such data in drawing inferences including a head-to-head comparison of two treatments. With that said, many observational studies could yield similar results to RCT (e.g., some of the work Miguel Hernan from Harvard). Plus, in my previous organization, my colleagues evaluated many pieces of evidence generated by RCTs about the effectiveness of drugs so we can include these drugs in our formularies. We had more Medicare population and many of the RCTs conducted either excluded older population or they were under-represented. Hence, we needed to see more evidence and we utilized “what we have” to see where the “direction” of the effect is going. This was not feasible for all disease areas but we had long records for many of our patients (>10 years). I guess the point I am trying to make here, a well-thought and meticulously planned observational studies could provide insight to decision making even with their inherited shortcomings. The level of certainty to base decision making using observational studies is inferior to RCT but important nevertheless
FH: Enrollment is a common problem in RCTs. It occurs frequently when patients and physicians think they already know what’s best for the patient, and they are constantly surprised when good RCTs disagree with prevailing beliefs. I can argue that clinical practice is experimentation without the protections afforded by RCTs. I say that because the treatment you get is so subject to ‘the luck of the draw’, e.g., which physician you select and what was the last paper or advertisement read by that physician. If patients really knew how little we learn from clinical practice and how much we learn from experimentation, they would flock even more to RCTs.
Note that some RCTs that were thought to be almost impossible turned out to have patients flock to them in great numbers, e.g., an ablation bronchoscope for refractory asthma, where patients know that they had a 1/2 chance of getting a sham bronchoscopy.
The amount of money we waste on ineffective treatments would fund all the RCTs we could handle.
Unknown: How often do you find that randomized controlled trials are performed as well as they are designed? For example, I have been trying to enroll patients in a trial that compares two different treatments; however, one is surgery with a 6-12 week recovery period and the other is a (serious but) less involved and has a faster recovery for the patient (1-2 week recovery but might not work as well long term.) I’ve yet to enroll any patients because most won’t make an informed decision to be randomized.
So although a multicenter RCT is underway and funded, its difficult to enroll patients. I don’t know if this difficulty to enroll patient will manifest in any study bias; however, it will definitely decrease the study’s power.
I haven’t been involved in many RCTs, so I don’t know how common this problem is.
FH: Often one can collect the needed baseline data in 1 or 2 pages of a case report form. The excessive cost of RCTs is not coming from that. It is coming from (1) endless site and data queries as you mentioned and (2) collection of data that are not central to the questions of interest and are almost never analyzed. It is amazing to see how much data collected in a trial are not used in key study reports or published articles. And the thousands of trials, if their data were to be be made publicly available, that would provide a scientific basis for HTE is stunning.
Unknown: If one buys the general thesis, the next big question is how much is the assiduous definition of baseline characteristics worth? Most of RCT budgets are being spent on endless detail and queries, including efforts to reconcile disparate clinical records. The trials are getting so expensive that they have become a major impediment to investment in major chronic disease therapies (some trials > $1 Billion for a single trial). is there an empirical way to calibrate the degree of precision needed at baseline (and for covariates in followup) relative to accurate measurement of critical outcomes that matter?