---
title: Equivalence of Wilcoxon Statistic and Proportional Odds Model
author:
- name: Frank Harrell
url: https://hbiostat.org
affiliation: Department of Biostatistics<br>Vanderbilt University School of Medicine
date: "2022-04-06"
modified: last-modified
categories: [2022, 2024, endpoints, ordinal, drug-evaluation, hypothesis-testing, RCT, regression]
description: "In this article I provide much more extensive simulations showing the near perfect agreement between the odds ratio (OR) from a proportional odds (PO) model, and the Wilcoxon two-sample test statistic. The agreement is studied by degree of violation of the PO assumption and by the sample size. A refinement in the conversion formula between the OR and the Wilcoxon statistic scaled to 0-1 (corcordance probability) is provided."
---
```{r include=FALSE}
source('~/rr/rmarkdown/qbookfun.r')
```
`r disccom('rms-ordinal-logistic-regression')`
# Introduction
The Wilcoxon-Mann-Whitney two-sample rank-sum test is a nonparametric test that is much used for comparing two groups on an ordinal or continuous response Y in a parallel group design. Here is how the Wilcoxon statistic is computed and is related to other measures. [[Comments](https://hbiostat.org/comment.html)]{.aside}
* Rank all $n$ observations, using midranks for ties
* The Wilcoxon statistic $W$ is the sum of the ranks for those observations belonging to the second group
* The Mann-Whitney statistic $U$ equals $W - \frac{m(m+1)}{2}$ where $m$ is the number of observations in the second group
* The concordance probability $c$, also called the _probability index_, is $U$ divided by the product of the two groups' sample sizes. $c$ treats ties as having a concordance of $\frac{1}{2}$, which stems from the use of midranks for ties in computing $W$. $c$ is the probability that a randomly chosen subject from the second group has a response Y that is larger than that of a randomly chosen subject from the first group, plus $\frac{1}{2}$ times the probability that they are tied on Y. $c$ is just the Wilcoxon statistic re-scaled to $[0,1]$.
The [proportional odds (PO) ordinal logistic model](https://hbiostat.org/bib/po) is a generalization of the Wilcoxon-Mann-Whitney two-sample rank-sum test that allows for covariates. When there are no covariates, the Wilcoxon test and PO model are equivalent in two ways:
* The numerator of the Rao efficient score test for comparing two groups in the unadjusted PO model, which tests for an odds ratio (OR) of 1.0, is identical to the Wilcoxon test statistic
* Over a wide variety of datasets exhibiting both PO and non-PO, the $R^2$ for predicting the logit of $c$ from the PO log(OR) is 0.996
This has been explored in two of my blog articles:
* [Violation of Proportional Odds is Not Fatal](https://fharrell.com/post/po)
* [If You Like the Wilcoxon test You Must Like the Proportional Odds Model](https://fharrell.com/post/wpo)
Those unfamiliar with the theory of linear rank statistics will sometimes make the claim that the Wilcoxon test does not assume proportional odds. That this is not the case can be seen in multiple ways:
* The OR from the PO model is almost exactly a simple monotonic function of the Wilcoxon statistic (the main topic of this article)
* The PO model score test and the Wilcoxon statistic are mathematically equivalent (see above) just as the score test from the Cox proportional hazards model is the same as the logrank test statistic
* As explained [here](https://myweb.uiowa.edu/pbreheny/uk/teaching/621/notes/9-27.pdf) by Patrick Breheny, linear rank tests such as the Wilcoxon test are derived in general by solving for the locally most powerful test. Each type of linear rank test comes from a generating distribution. Here are some examples:
+ Normal generating distribution: the optimal weight for the rank $r$ of the response variable is the expected value of order statistic $r$ from a standard normal distribution (Fisher-Yates normal scores) or their approximation $\Phi^{-1}(\frac{r}{n+1})$ (van der Waerden scores). The semiparametric model counterpart is the probit ordinal regression model
+ Double exponential (Laplace) distribution: the observation weight is $\mathrm{sign}(r - \frac{n+1}{2})$ (Mood median test or sign test)
+ Logistic distribution: optimal weights are the ordinary ranks $r$. The logistic generating distribution means the two distributions are parallel on the inverse logistic (logit) scale, i.e., PO holds
So the Wilcoxon test is designed for a logistic distribution/PO situation, i.e, that is where it has the most power. Hence it is fair to say that the Wilcoxon test assumes PO. The statement that the Wilcoxon test does not assume PO in order to validly compute $p$-values is misleading; under the null hypothesis the treatment is irrelevant so it **must** operate in proportional odds. It must also simultaneously operate in proportional hazards and under a wide variety of other model assumptions. Since treatment doesn't affect the distribution of Y under the null, there are no distribution shift assumptions.
The Wilcoxon two-sample test, invented in 1945, is embraced by most statisticians and clinical trialists, and it doesn't matter to them whether the test assumes PO or not. Our argument is that since the unadjusted PO model is equivalent to the Wilcoxon test, any reviewer accepting of the Wilcoxon test should logically be accepting of the PO model (invented in 1967). The only possible criticism would be that adjusting for covariates that do not satisfy the PO assumption would ruin the assessment of the treatment effect in the PO model. That this is not the case is demonstrated by an extreme non-PO example [here](https://fharrell.com/post/impactpo).
In this report I go a step further that earlier blog articles and repeat the simulations done with more repetitions and many more conditions and stratify the results by the degree of non-proportional odds exhibited in each random sample. Random trials were simulated for sample sizes 20, 25, 30, 40, 50, 60, ..., 100, 150, 200, 500, 1000. For each trial, 0:1 group assignments were generated such that the number of subjects in the first treatment group is $n \times u$ rounded to the nearest integer, where $u$ is a random uniform value between $\frac{1}{3}$ and $\frac{2}{3}$ . Ordinal responses Y were generated in five ways by using combinations of the following two aspects:
* More continuous vs. more discrete Y
+ sampling with replacement from the integers 1 to n for the current sample size n
+ sampling with replacement from the integers 1 to m where for each trial m is randomly chosen from the integers 4, 5, 6, ..., 10
* Equal vs. unequal sampling probabilities vs. normal distributions with unequal variances
+ Equal sampling probabilities for both groups and all levels of Y. This is for a null case where there are no true group differences, and will generate samples showing non-PO only for smaller trials
+ Unequal sampling probabilities, allowing arbitrarily large (or null) treatment effects and arbitrarily large (or small) non-PO for all sample sizes. This is done by taking a random sample of size n or m from a uniform distribution, taking these as the multinomial probabilities for Y in the first group, sampling n0 Y from these unequal probabilities. Then repeat the process independently for the second group with n1 observations. The two sets of multinomial probabilities are disconnected, allowing arbitrarily large non-PO.
+ Sampling from two normal distributions with varying true differences in means and varying ratios of standard deviations. For this case, large non-PO occurs when the SDs are much different. Trial data for the number of participants assigned to the first group are simulated from a normal distribution with mean $\mu$ and SD $\sigma$ where $\mu$ is a draw from a uniform distribution ranging over -1.5 to 1.5 and $\sigma$ is a draw from a uniform distribution ranging over 0.4 to 3.0. Then new single draws are made for $\mu$ and $\sigma$ for the second sample, and the sample is similarly drawn from a normal distribution. Both sets of sample values are multiplied by ten and rounded to the nearest integer. For this type of random number generation, n vs. m is ignored so there are more simulations for this third type.
One hundred trials are run for each sample size and for each of five combinations. This process generates many configurations of ties and distinct values of Y, degrees of non-proportionality, and treatment allocation ratios.
But before approximating the Wilcoxon statistic from the odds ratio in a PO model let's first consider an exact result when PO holds.
# Analytic Concordance Probability From a PO Model
[De Neve, Thas, and Gerds](https://onlinelibrary.wiley.com/doi/abs/10.1002/sim.8078) derived the concordance probability (probability index; PI) for several generating distributions. The context is transformation models, a way of restating semiparametric models by specifying a parametric distribution for an unknown monotonic transformation of Y. In transformation models, the effect of a predictor represents a shift in the transformed distribution. When the parametric distribution is an extreme value type I distribution (the basis for the Cox proportional hazards model), the PI is, oddly enough, the logistic function. The distribution shift can be translated into a hazard ratio. When the generating distribution is the logistic distribution, the shift on the transformed Y scale represents what happens with a PO model, and the PI is more complex. Letting $r$ denote the odds ratio, and thinking of the PI more generally as the probability that two Y's are in order given two covariate vectors $X_{1}, X_{2}$, the general form of the PI is [The PI from a PO model is exemplified in [Tian et al](https://onlinelibrary.wiley.com/doi/abs/10.1002/sim.8425).]{.aside}
$$\Pr(Y_{1} < Y_{2} | X_{1}, X_{2}) = G((X_{2} - X_{1})\beta)$$
and for the logistic case we get the PI from their Table 1 as
$$\Pr(Y_{1} < Y_{2} | X_{1}, X_{2}) = \frac{r(r - log(r) - 1)}{(r - 1) ^ {2}}$$
where $r$ is $\exp(\beta)$ and $\beta$ is the regression coefficient for treatment.
Note that the general form allows consideration of covariate-adjusted treatment comparisons, i.e., $X$ is a vector and only the treatment variable changes when constructing $X_1$ and $X_2$.
Based on the simulations to approximate Wilcoxon statistics for the not-necessarily-PO case below, and recalling that the Wilcoxon setup has $X$ is a treatment group indicator ($X_{2}=1, X_{1}=0$), I attempted to approximate the PI using $\frac{r ^ \alpha}{1 + r ^ \alpha}$ for odds ratios $r$ between $\frac{1}{10}$ and $10$. The best approximating value was $\alpha = 0.675$ resulting in a maximum error in approximating the PI (concordance probability) of only 0.0013. Keep this value of $\alpha$ in mind as we return to the main task at hand, to _numerically_ compute the Wilcoxon statistic from a PO models' _estimated_ OR **whether or not PO holds**.
```{r}
f <- function(z) {
r <- exp(z)
r * (r - z - 1)/((r - 1)^2)
}
f(.01)
f(.001)
f(.0001)
f(.00001)
r <- seq(.1, 10, length=1000)
g <- function(a) max(abs(r ^ a / (1 + r ^ a) - f(log(r))))
optimize(g, c(.6, .7), tol=1e-9)
```
Before trying to compute the observed Wilcoxon statistic from an observed odds ratio, let's first figure out how to quantify the amount of non-PO that is present in a given dataset. That way we'll be able to see if the equivalence of the PO model and the Wilcoxon test statistic still holds in severe non-PO situations.
# Quantifying the Departure from PO
For a given sample the degree of non-PO is quantified using the following steps:
* Compute the empirical cumulative distribution function (ECDF) of Y stratified by group assignment
* Evaluate these ECDFs at the combined set of distinct Y values occurring in the data for either group
* When an ECDF value is outside [0.02, 0.98] set it to that nearest boundary
* Take the logits of the two ECDFs
* Compute over the grid of combined distinct values the difference between the two logit CDFs to examine parallelism. Parallel curves on the logit scale indicate PO.
* Quantify the non-parallelism by taking Gini's mean difference of all the differences (a robust competitor of the standard deviation that is the mean of all pairwise absolute differences). A low value indicates parallelism. The lowest possible value of 0.0 indicates equidistant logit ECDFs across all values of Y.
This procedure is virtually the same as computing empirical log odds ratios for all possible cutoffs of Y and looking at their variation. It differs only in how differences are computed for a cutpoint that is outside the data for one of the groups. It may give too much weight to unstable ORs, so also compute a second measure of non-PO, not using any extrapolation, that is a weighted standard deviation of log ORs over all cutoffs of $Y$, with weights equal to the estimated variance of the log odds ratios. This index can be computed whenever there are at least two cutpoints having neither 0.0 nor 1.0 proportions in either group.
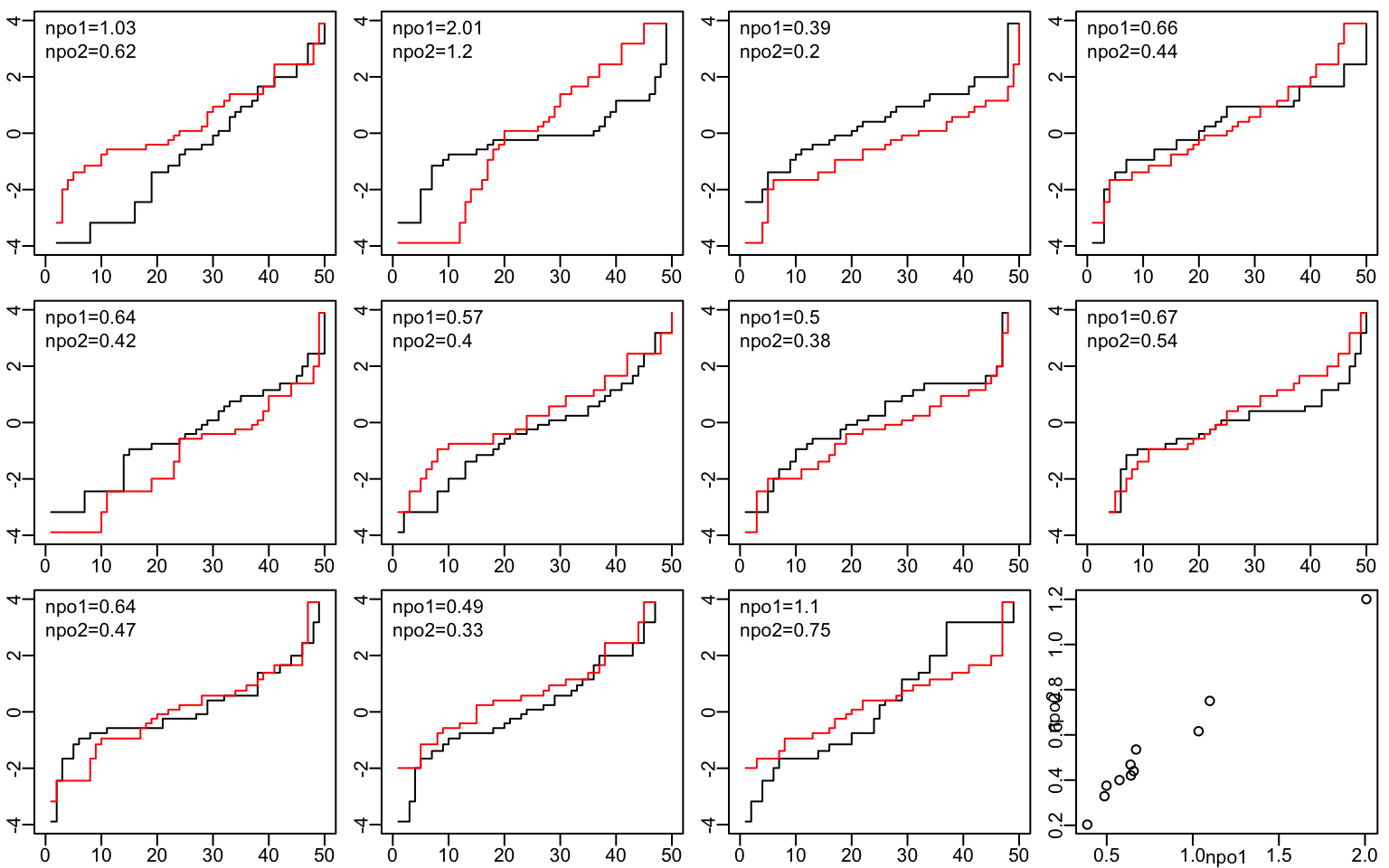
The indexes of non-PO are exemplified by taking samples of size n=50 in a similar way to how the simulation will be run later. The plotted ECDFs for the two groups are on the logit scale. The index of non-parallelism of these two transformed curves appears on each panel. The bottom right panel shows the relationship of the two indexes.
```{r setup,include=FALSE}
require(rms)
```
```{r illusnonpo,fig.width=8,fig.height=5}
# Function to curtail to [0.02, 0.98] before taking logit
lg <- function(p) qlogis(pmax(pmin(p, 1. - 0.02), 0.02))
# Function to curtail log ORs to [-6, 6]
cu <- function(x) pmin(pmax(x, -6), 6)
# Function to quantify degree of non-proportional odds first by computing the
# Gini's mean difference of the difference between
# two logit of ECDFs. Quantifies variability of differences over y
# When ECDF is 0 or 1 replace by 0.02, 0.98 so can take logit
# Note that ecdf produces a function and when it is called with an
# x-value that outside the range of the data the value computed is 0 or 1
# Computes a second index of non-PO by getting a weighted standard deviation of
# all possible log ORs, where weights are inverse of variance of log OR
# Note that when a P(Y>=y) is 0 or 1 the weight is zero because variance is infinite.
npod <- function(y1, y2, pl=FALSE, xlim=range(ys),
ylim=range(lg(f1(r)), lg(f2(r))), axes=TRUE) {
f1 <- ecdf(y1)
f2 <- ecdf(y2)
y <- c(y1, y2)
r <- range(y)
ys <- sort(unique(y))
# There cannot be non-PO if only 2 levels of y, and if no overlap
# there is no way to assess non-PO
if(length(ys) <= 2 || max(y1) <= min(y2) || max(y2) <= min(y1))
npo1 <- npo2 <- 0.
else {
dif <- lg(f1(ys)) - lg(f2(ys))
npo1 <- GiniMd(dif)
lor <- w <- numeric(length(ys) - 1)
n1 <- length(y1)
n2 <- length(y2)
for(j in 2:length(ys)) {
y <- ys[j]
p1 <- mean(y1 >= y)
p2 <- mean(y2 >= y)
if(min(p1, p2) == 0 || max(p1, p2) == 1) lor[j-1] <- w[j-1] <- 0
else {
lor[j-1] <- log(p2 / (1. - p2)) - log(p1 / (1. - p1))
w [j-1] <- 1. / ((1. / (n1 * p1 * (1. - p1))) +
(1. / (n2 * p2 * (1. - p2))))
}
}
npo2 <- sqrt(wtd.var(lor, w, normwt=TRUE))
}
if(pl) {
plot (ys, lg(f1(ys)), type='s', xlab='', ylab='',
xlim=xlim, ylim=ylim, axes=axes)
lines(ys, lg(f2(ys)), type='s', col='red')
text(xlim[1], ylim[2],
paste0('npo1=', round(npo1, 2), '\nnpo2=', round(npo2, 2)),
adj=c(0,1))
}
c(npo1=npo1, npo2=npo2)
}
require(qreport) # defines kabl, htmlList
n <- 50; n0 <- n1 <- 25
par(mfrow=c(3,4), mar=c(1.5,1.5,.5,.5), mgp=c(.5, .4, 0))
set.seed(368)
z <- matrix(NA, nrow=11, ncol=2)
for(i in 1 : 11) {
p0 <- runif(n)
# Note that sample uses prob as weights and they need not sum to 1
y0 <- sample(1 : n, n0, prob=p0, replace=TRUE)
p1 <- runif(n)
y1 <- sample(1 : n, n1, prob=p1, replace=TRUE)
z[i, ] <- npod(y0, y1, pl=TRUE, xlim=c(0, 50), ylim=c(-4, 4))
}
plot(z[, 1], z[, 2], xlab='npo1', ylab='npo2')
```
# Simulation
```{r simset}
sim <- function() {
require(MASS)
N <- nrow(d)
cstat <- beta <- npo <- npo2 <- numeric(N)
ydiscrete <- logical(N)
type <- character(N)
worst <- list()
iworst <- 0
largenpo <- list()
ilarge <- 0
for(i in 1 : N) {
n <- d[i, 'n']
dis <- d[i, 'ydiscrete']
ty <- d[i, 'type']
# Don't allow more than a 2:1 imbalance
n0 <- round(n * runif(1, 1/3, 2/3))
n1 <- n - n0
x <- c(rep(0, n0), rep(1, n1))
numcat <- if(dis) sample(4:10, 1, replace=TRUE) else n
switch(ty,
null = {
y <- sample(1 : numcat, n, replace=TRUE)
y0 <- y[1 : n0]
y1 <- y[(n0 + 1) : n] },
unequalp = {
# Simulate each group separately, with disconnected cell probabilities
p0 <- runif(numcat)
y0 <- sample(1 : numcat, n0, prob=p0, replace=TRUE)
p1 <- runif(numcat)
y1 <- sample(1 : numcat, n1, prob=p1, replace=TRUE)
y <- c(y0, y1) },
cont = {
# Simulate two samples from normal distributions with
# different means and variances, and round
mu0 <- runif(1, -1.5, 1.5)
s0 <- runif(1, 0.4, 3)
y0 <- round(rnorm(n0, mu0, s0) * 10)
mu1 <- runif(1, -1.5, 1.5)
s1 <- runif(1, 0.4, 3)
y1 <- round(rnorm(n1, mu1, s1) * 10)
y <- c(y0, y1)
# cat(round(length(unique(y)) / length(y), 1), '',
# file='/tmp/z', append=TRUE)
} )
cstat[i] <- (mean(rank(y)[x == 1]) - (n1 + 1) / 2) / n0
b <- coef(orm(y ~ x, eps=0.000001, maxit=25, tol=1e-14))
beta[i] <- b[length(b)]
np <- npod(y0, y1)
npo[i] <- np[1]
npo2[i] <- np[2]
type[i] <- ty
ydiscrete[i] <- dis
or <- exp(beta[i])
pcstat <- (or ^ 0.65) / (1 + or ^ 0.65)
err <- abs(pcstat - cstat[i])
if(err > 0.075) {
iworst <- iworst + 1
worst[[iworst]] <-
list(n0=n0, n1=n1, y0=y0, y1=y1, beta=beta[i],
npo=npo[i], npo2=npo2[i], cstat=cstat[i], pcstat=pcstat)
}
if(npo[i] >= 2.5) {
ilarge <- ilarge + 1
largenpo[[ilarge]] <- list(n0=n0, n1=n1, npo=npo[i], npo2=npo2[i],
y0=y0, y1=y1,
cstat=cstat[i], pcstat=pcstat)
}
}
list(cstat=cstat, beta=beta, ydiscrete=ydiscrete, type=type,
npo=npo, npo2=npo2, worst=worst, largenpo=largenpo)
}
seed <- 5
set.seed(seed)
ns <- c(20, 25, seq(30, 100, by=10), 150, 250, 500, 1000)
d <- expand.grid(n=ns, m=1:100, ydiscrete=c(FALSE,TRUE),
type=c('null', 'unequalp', 'cont'),
stringsAsFactors=FALSE)
w <- runifChanged(sim, npod, seed, ns, d, file='~/data/sim/powilcoxon.rds')
cstat <- w$cstat
beta <- w$beta
npo <- w$npo
npo2 <- w$npo2
worst <- w$worst
largenpo <- w$largenpo
ydiscrete <- w$ydiscrete
type <- w$type
```
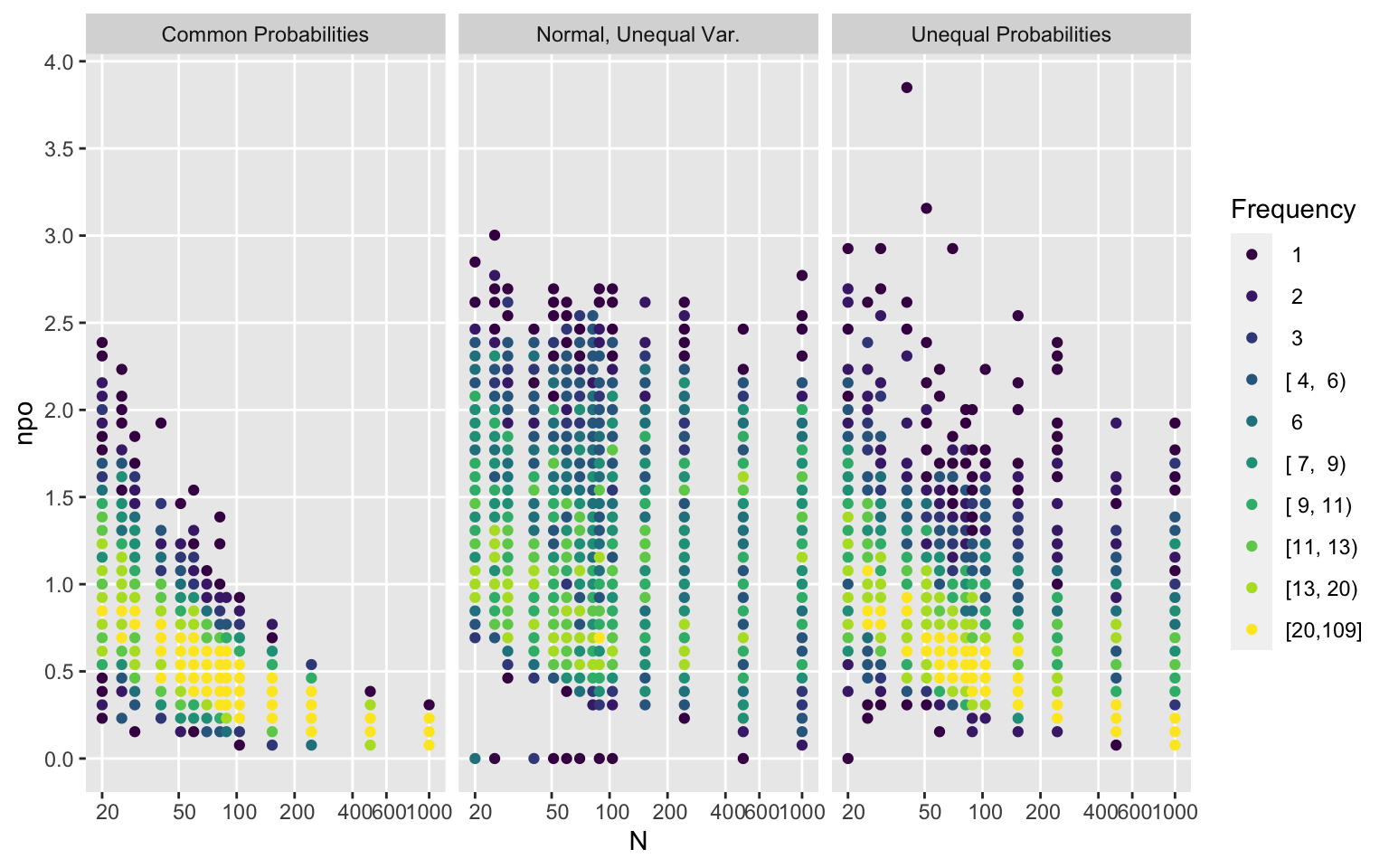
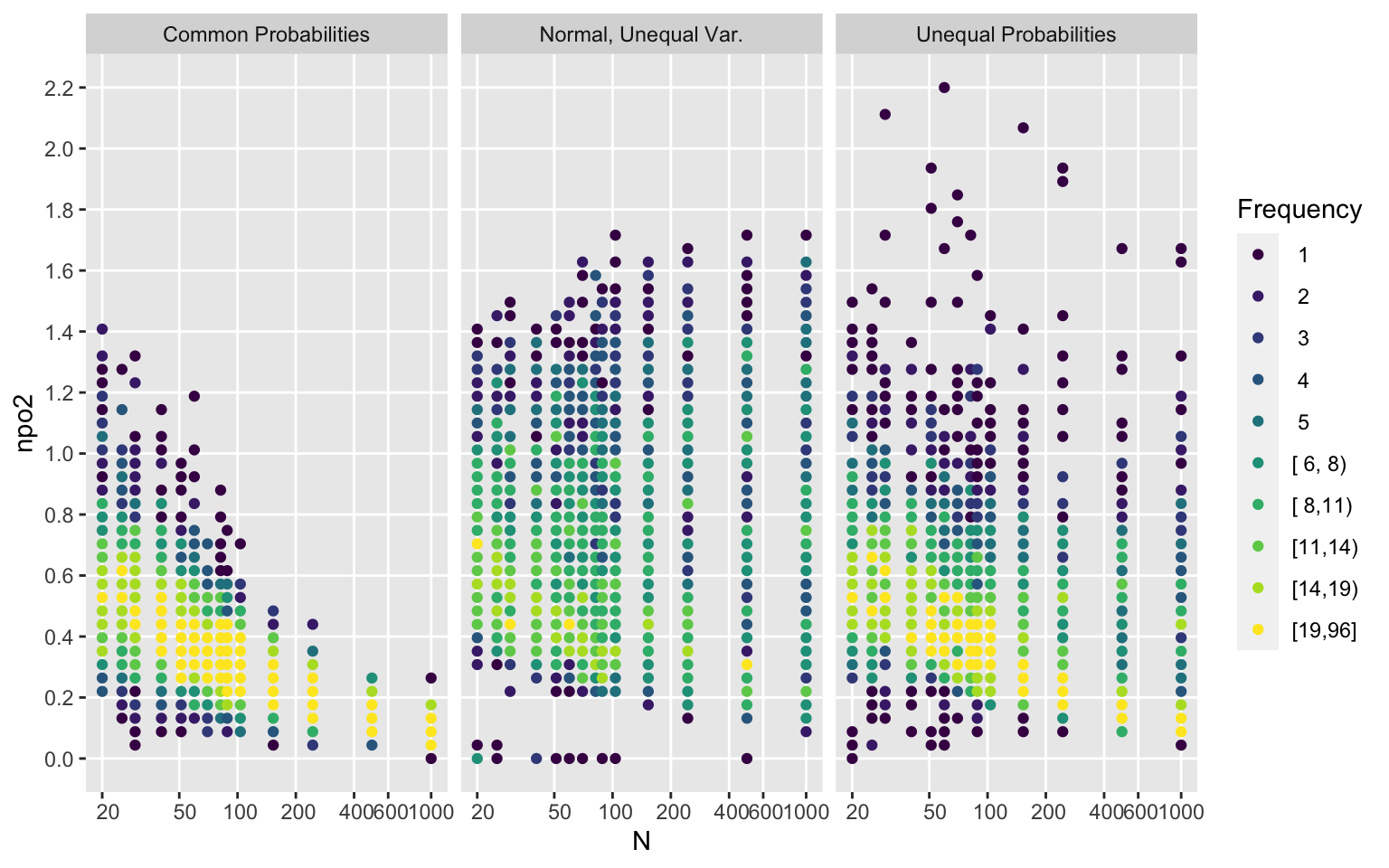
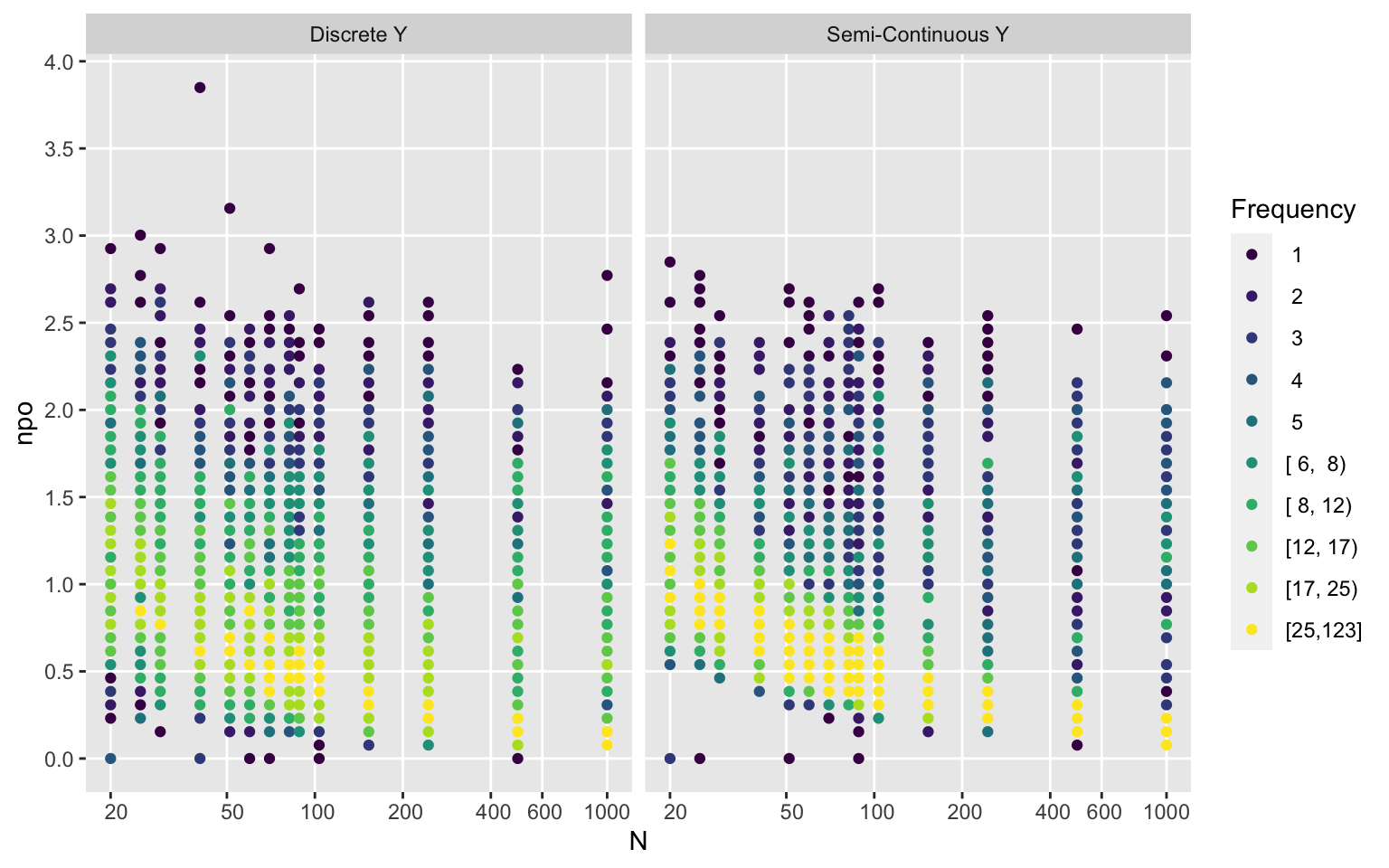
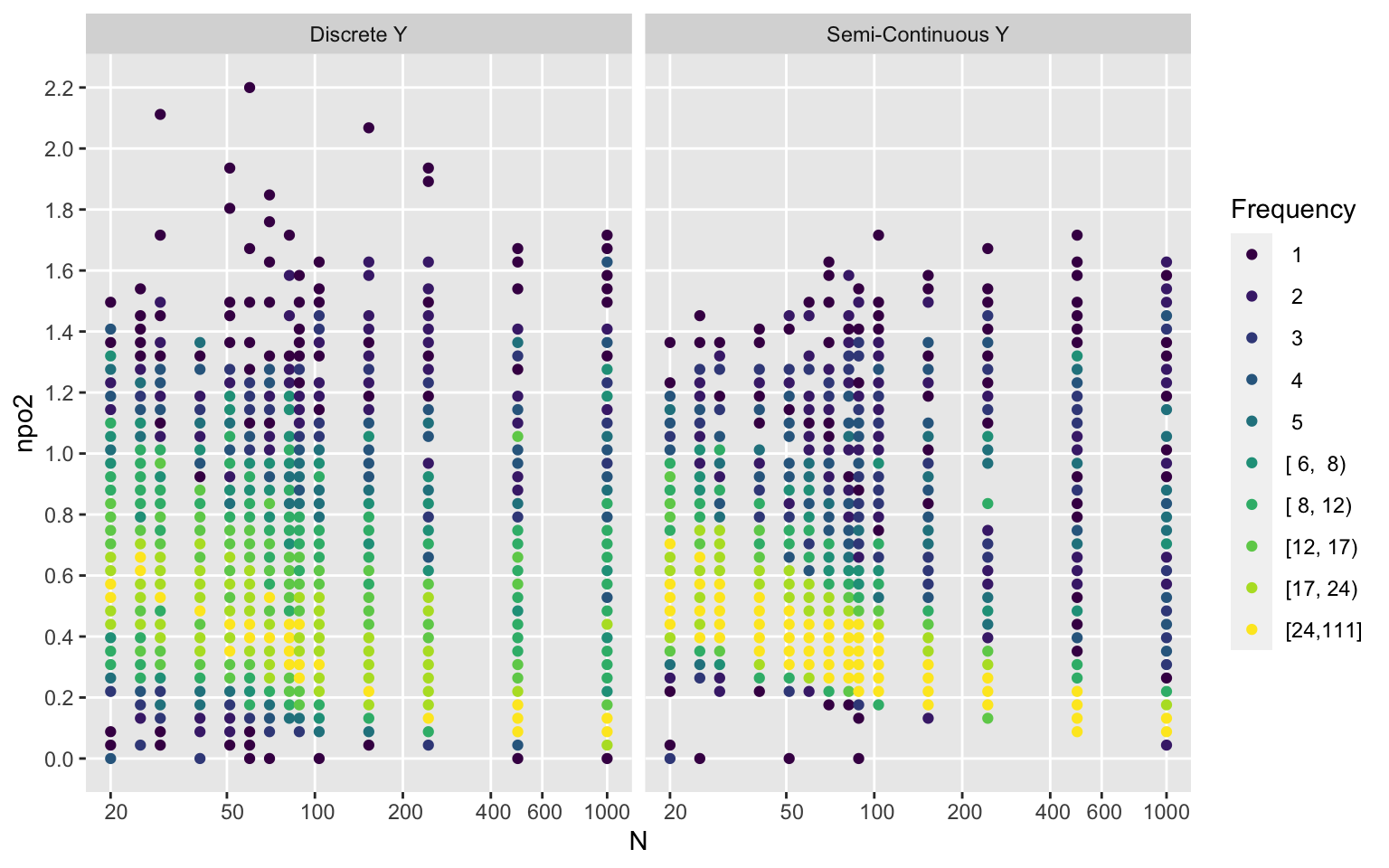
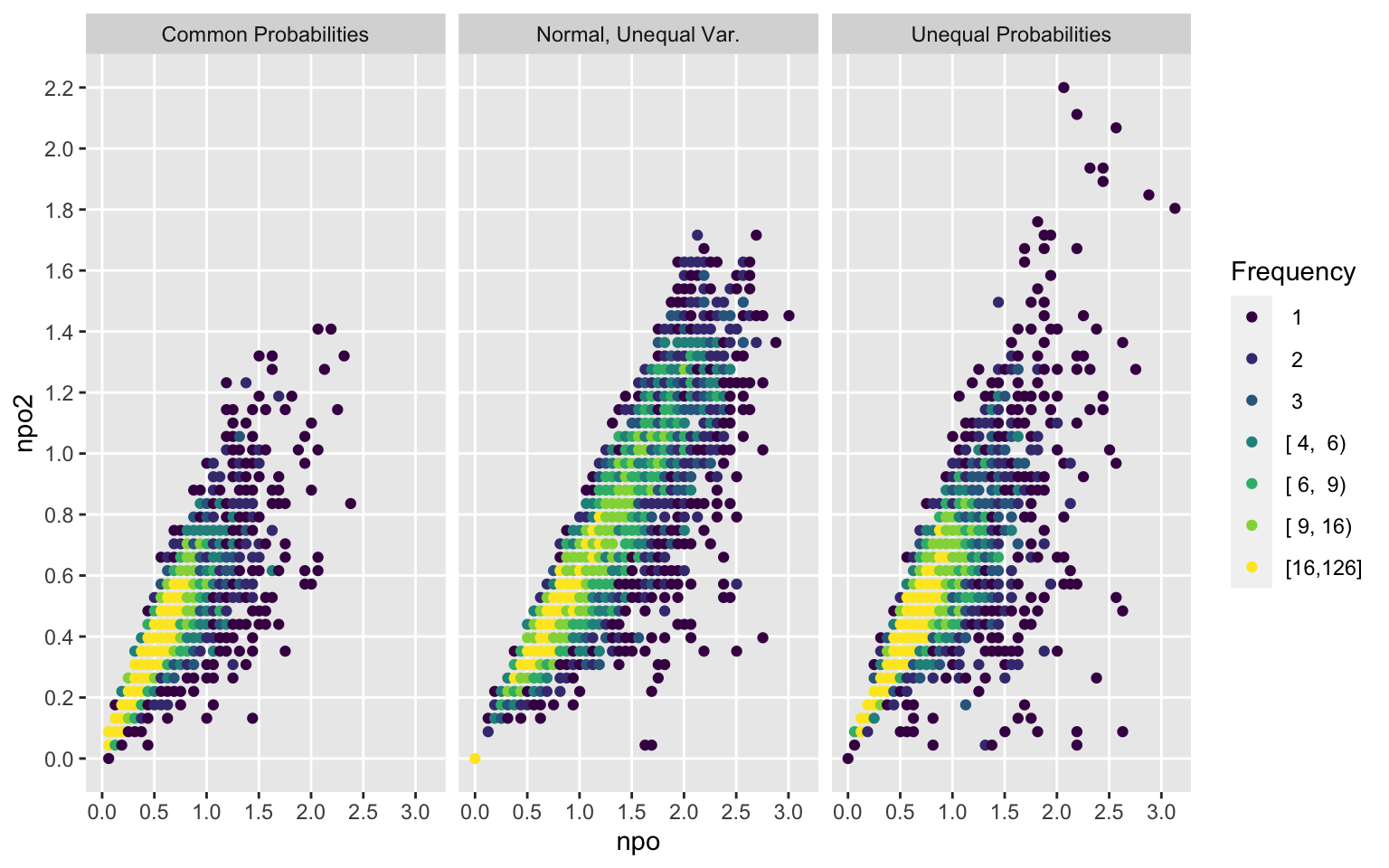
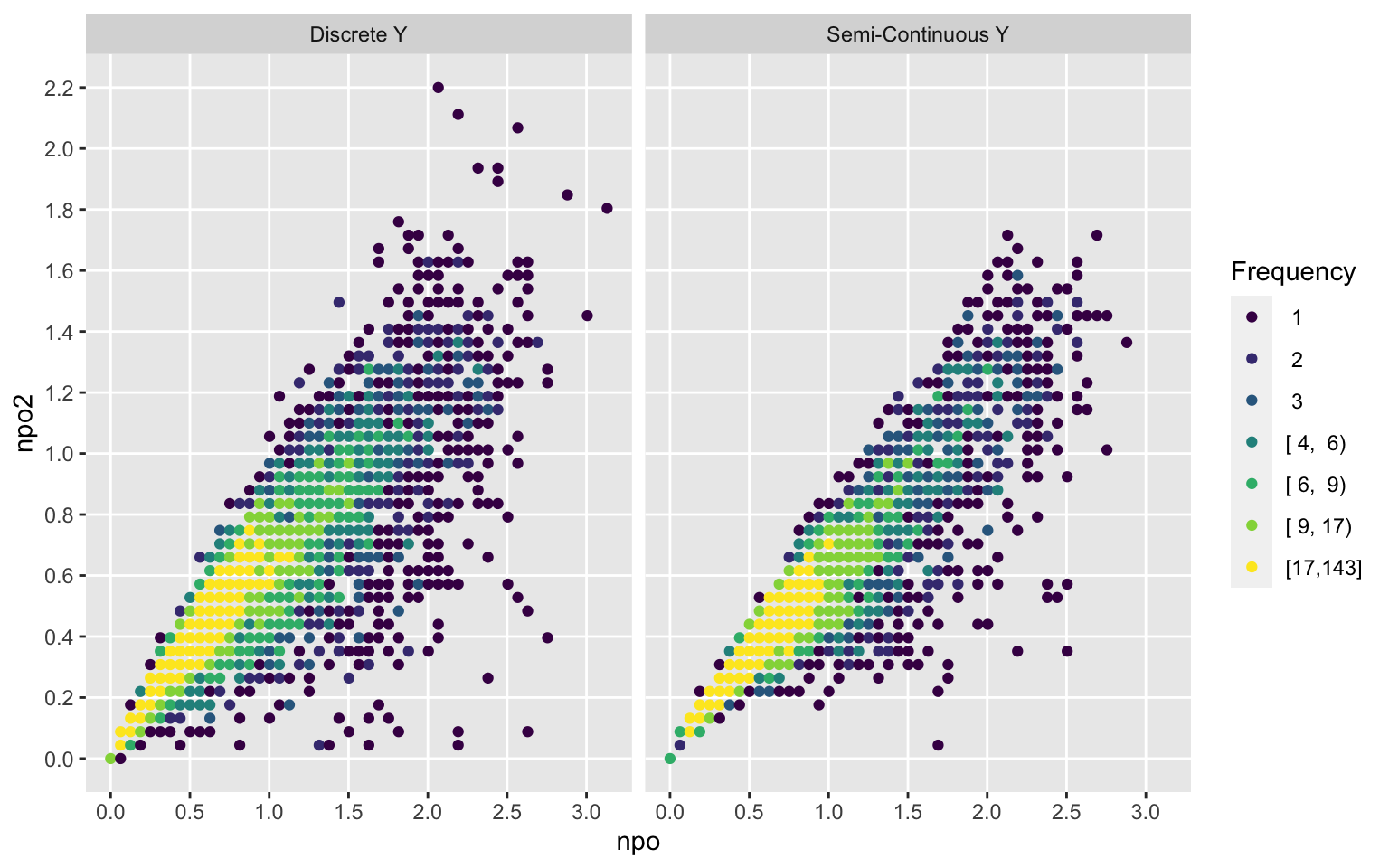
Examine how much non-PO is present in the simulated samples as a function of the sample size and the sampling strategy. Show this for two different non-PO measures, and see how the measures relate to each other.
```{r qnpo,fig.width=8}
Type <- c(null='Common Probabilities', unequalp='Unequal Probabilities',
cont='Normal, Unequal Var.')[type]
xb <- c(20, 50, 100, 200, 400, 600, 1000)
ggfreqScatter(d$n, npo, by=Type, xlab='N',
xbreaks=xb, xtrans=log)
ggfreqScatter(d$n, npo2, by=Type, xlab='N',
xbreaks=xb, xtrans=log)
Ydiscrete <- ifelse(ydiscrete, 'Discrete Y', 'Semi-Continuous Y')
ggfreqScatter(d$n, npo, by=Ydiscrete, xlab='N', xbreaks=xb, xtrans=log)
ggfreqScatter(d$n, npo2, by=Ydiscrete, xlab='N', xbreaks=xb, xtrans=log)
ggfreqScatter(npo, npo2, by=Type)
ggfreqScatter(npo, npo2, by=Ydiscrete)
kor <- function(a, b)
c(r = cor(a, b, use='complete.obs'),
rho = cor(a, b, method='spearman', use='complete.obs'))
kor(npo, npo2)
```
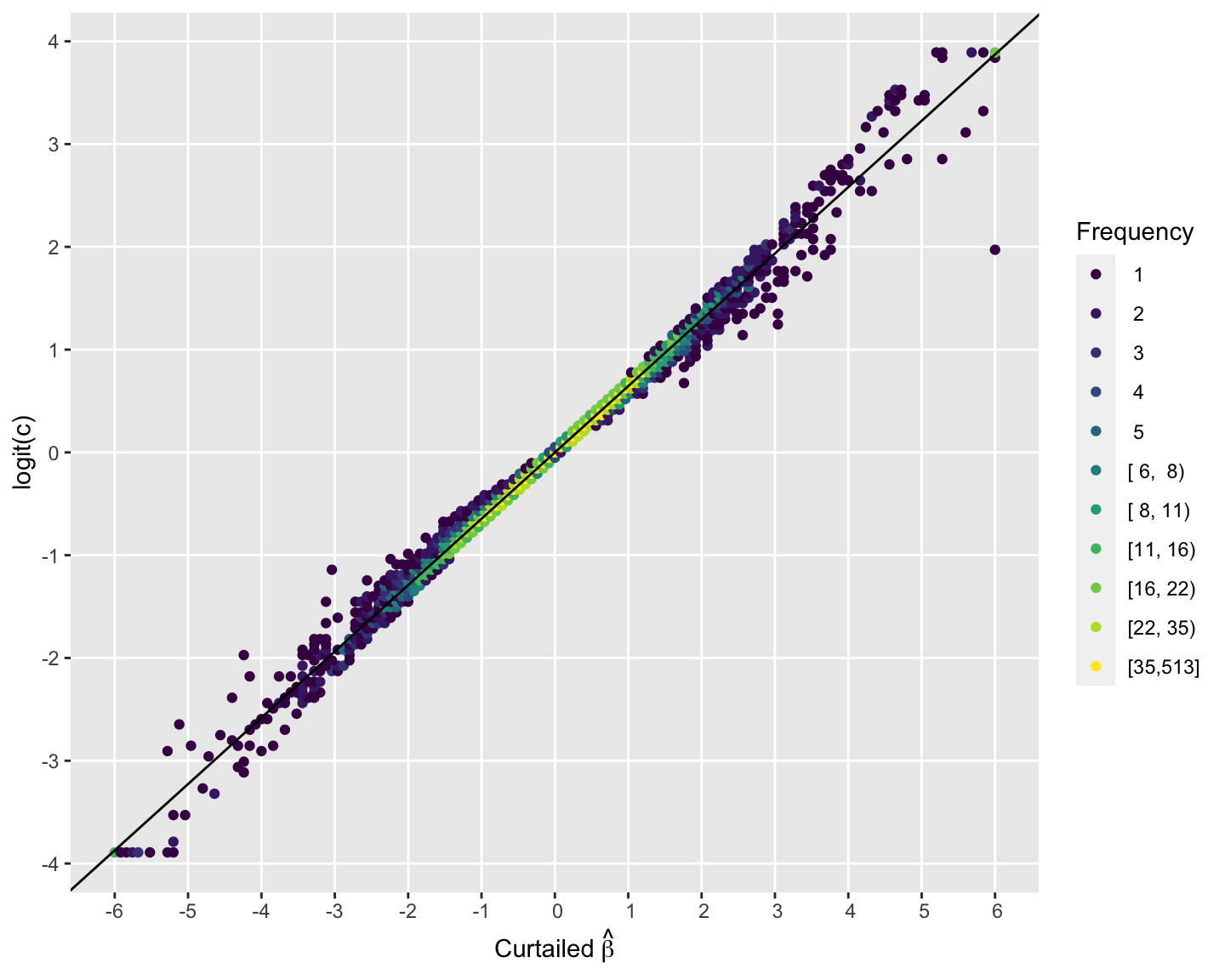
To derive the approximating equation for computing the concordance probability use robust regression to predict logit of concordance probability from the PO log(OR). $c$ is curtailed to $[0.02, 0.98]$ before taking the logit to not allow infinite estimates.
$\mathrm{logit}(c)$ is the chosen transformation because it transforms $c$ to be on an unrestricted scale, just as the log odds ratio is. By good fortune (or some unknown theoretical argument) this happens to yield almost perfect linearity.
::: {`r mNote`}
Quadratic and cubic polynomials were tried on the robust regression fit, with no improvement in $R^2$ or mean absolute prediction error.
:::
```{r robr,fig.height=6,fig.width=7.5}
g <- function(beta, concord, subset=1:length(beta)) {
require(MASS)
beta <- beta[subset]
concord <- concord[subset]
i <- ! is.na(concord + beta)
concord <- concord[i]
beta <- beta[i]
f <- rlm(lg(concord) ~ beta)
w <- ggfreqScatter(cu(beta), lg(concord), bins=150, g=20, ylab='logit(c)',
xlab=expression(paste('Curtailed ', hat(beta)))) +
geom_abline(intercept=coef(f)[1], slope=coef(f)[2])
print(w)
pc <- plogis(fitted(f))
dif <- abs(concord - pc)
w <- c(mean(dif, na.rm=TRUE), quantile(dif, 0.9, na.rm=TRUE), cor(pc, concord)^2)
names(w) <- c('MAD', 'Q9', 'R2')
list(Stats=w, Coefficients=coef(f))
}
w <- g(beta, cstat)
kabl(w$Stats, w$Coefficients)
agreeDirection <- (cstat == 0.5 & abs(beta) < 1e-7) | (cstat > 0.5) == (beta > 0)
```
MAD is the mean absolute difference between predicted and observed $c$, and Q9 is the 0.9 quantile of the absolute errors. Both measures are computed on the [0,1] scaled $c$.
The intercept is virtually zero and the regression coefficient of the log(OR) is 0.6453. Our approximation equation for computing the scaled Wilcoxon statistic from the PO model estimate of the OR is derived as follows:
* $\mathrm{logit}(c) = 0.6453 \log(\mathrm{OR})$
* $\frac{c}{1 - c} = \mathrm{OR}^{0.6453}$
* $c = \frac{\mathrm{OR}^{0.6453}}{1 + \mathrm{OR}^{0.6453}}$
::: {`r mNote`}
Note that with *probit* ordinal regression there is an exact analytic result due to [Agresti and Kateri](https://www.onlinelibrary.wiley.com/doi/10.1111/biom.12565) that applies even under covariate adjustment: $\Phi^{-1}(c) = \frac{\beta}{\sqrt{2}} \approx 0.707\beta$ as compared to our $0.6453\beta$. There is no known analytic result for the PO model. As an interesting aside, $\frac{\frac{1}{\sqrt{2}}}{0.6453} \approx 1.096$ which is not close to 1.6, the [scaling constant that makes the logistic distribution most similar to the normal distribution](https://www.johndcook.com/blog/2010/05/18/normal-approximation-to-logistic).
:::
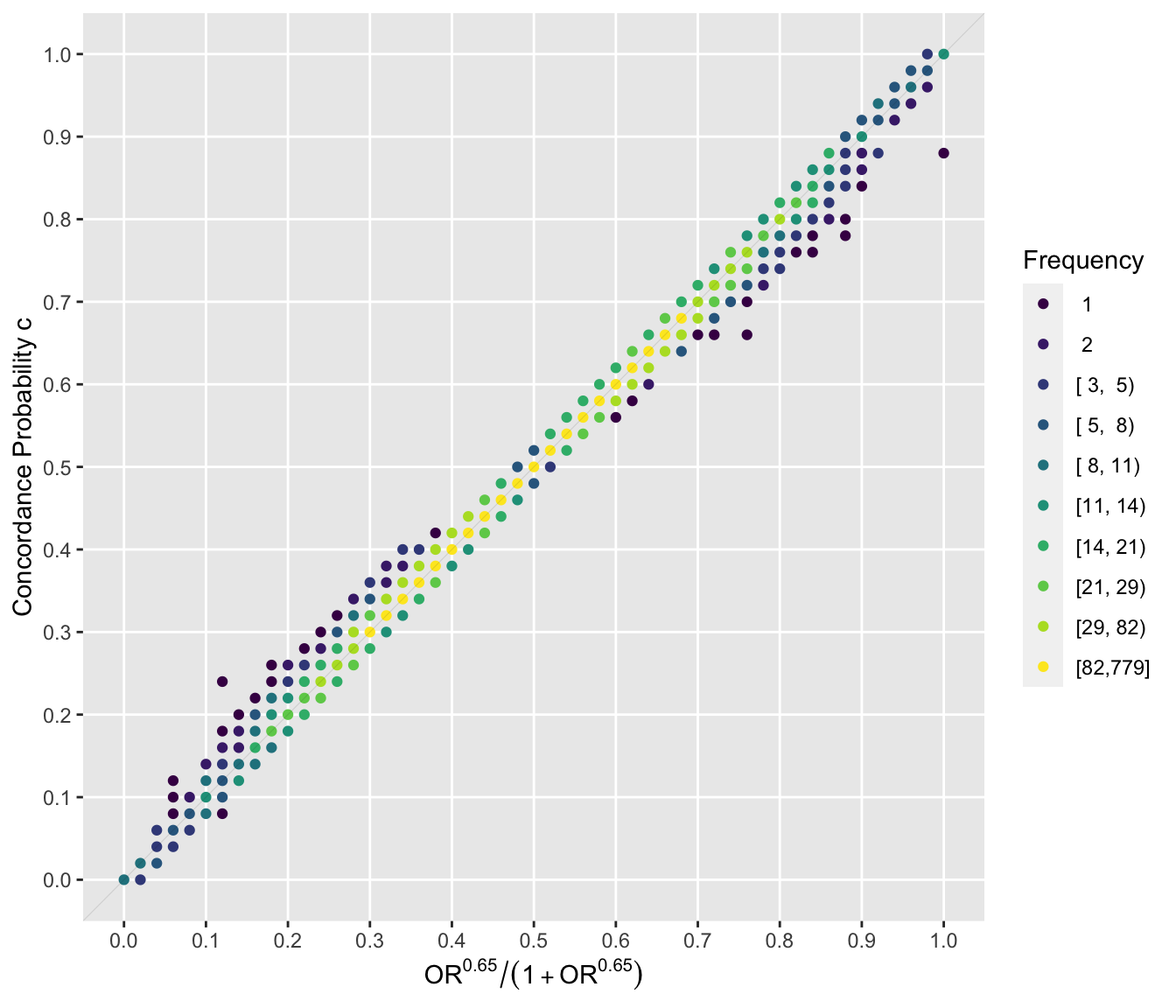
From here on the constant 0.65 will be used. Now examine the relationship on the concordance probability scale. The scatterplot uses colors to denote the frequency of occurrence of nearly coincident points. The quality of the approximation on this scale is given by $R^{2}=0.996$.
```{r acc,fig.height=6,fig.width=7,results='asis'}
ac <- function(b) {
or <- exp(b)
(or ^ 0.65) / (1 + or ^ 0.65)
}
ad <- abs(cstat - ac(beta))
h <- function(x) round(mean(x), 4)
MAD <- ad
s <- summary(MAD ~ Ydiscrete + Type, fun=h)
print(s, markdown=TRUE)
xl <- expression(OR ^ 0.65 / (1 + OR ^ 0.65))
yl <- 'Concordance Probability c'
ggfreqScatter(ac(beta), cstat, xlab=xl, ylab=yl) +
geom_abline(intercept=0,slope=1,alpha=.1,size=.2)
```
::: {`r mNote`}
The points that are more consistent with a curved relationship are mostly singletons or frequency 2-4.
:::
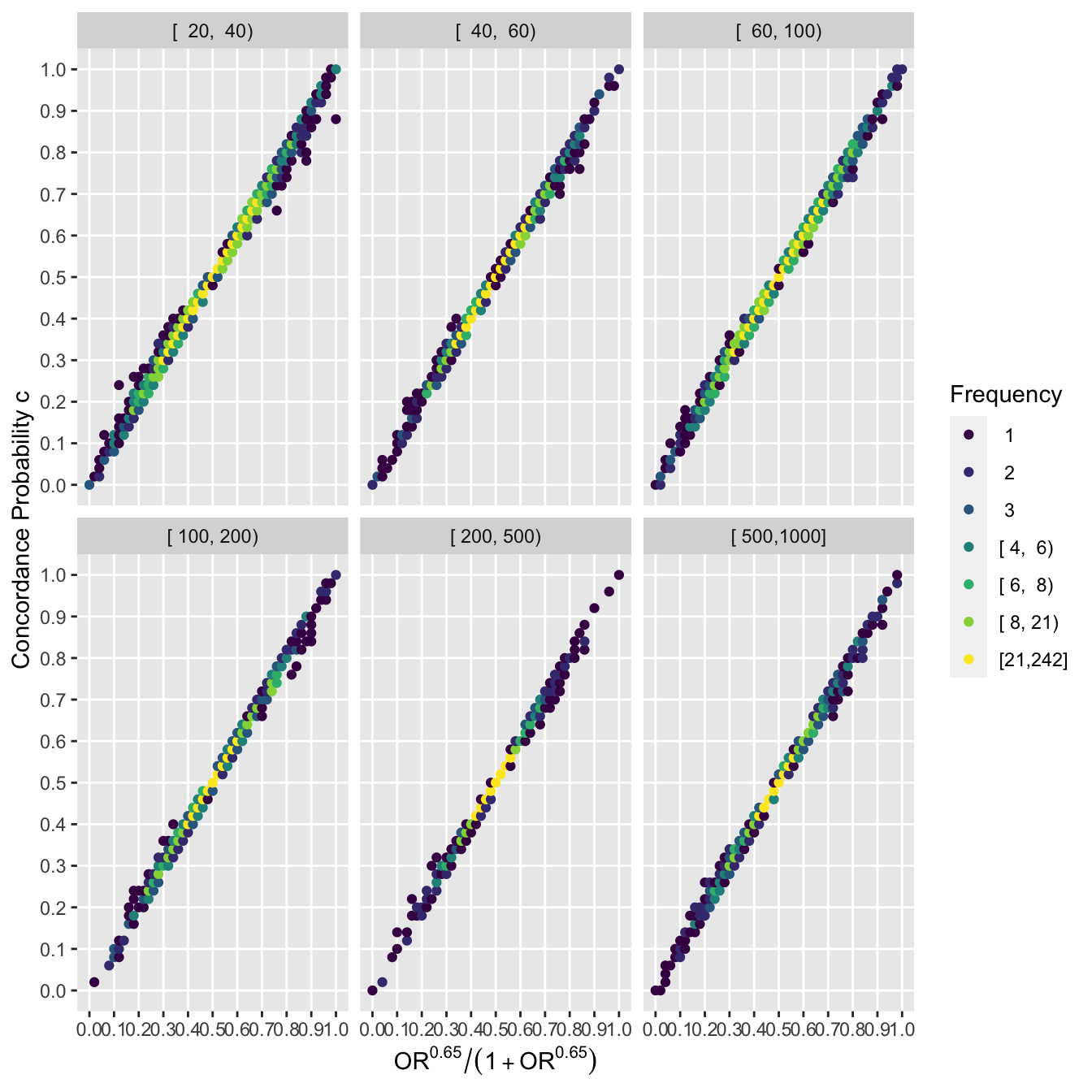
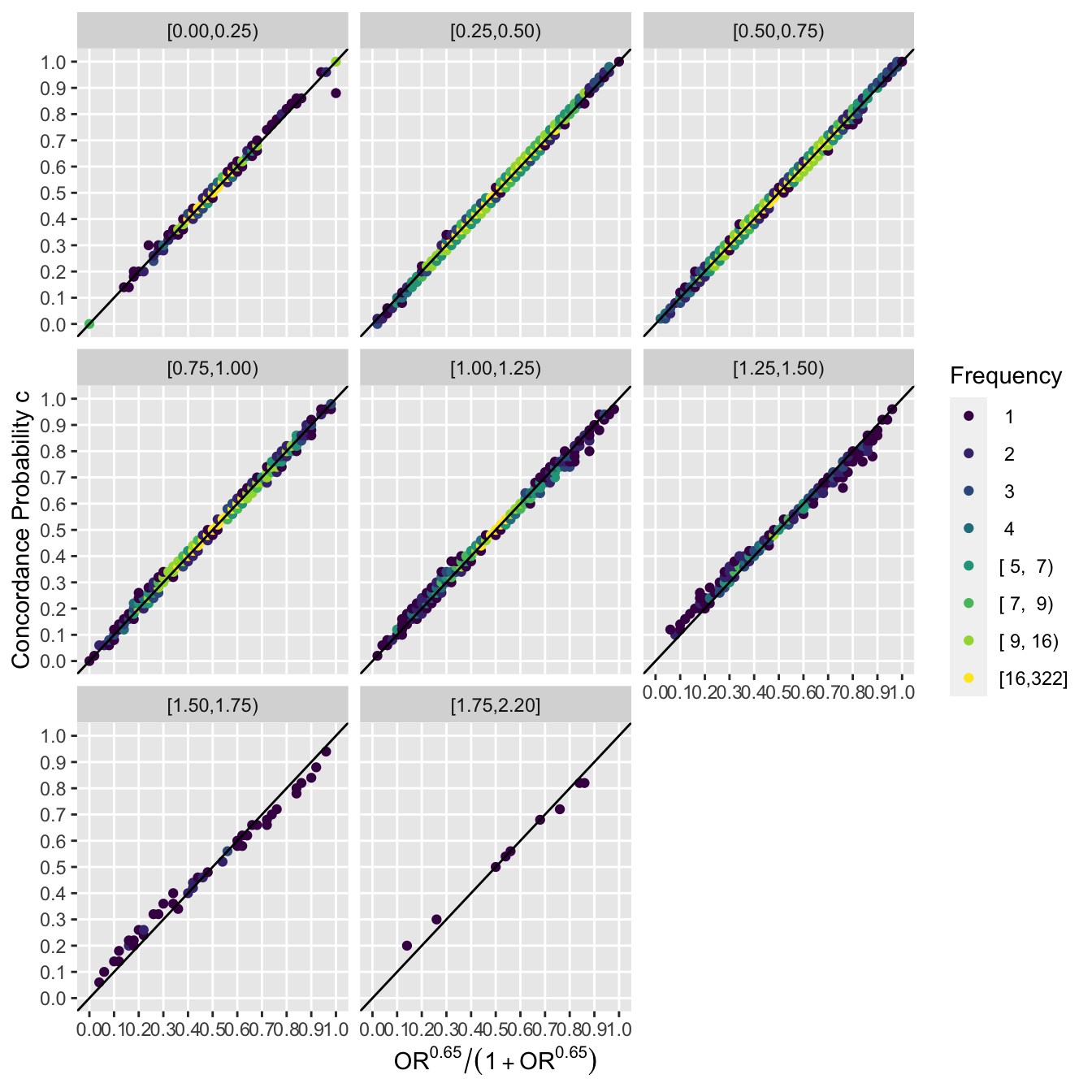
Repeat the last graph stratified by intervals of study sample sizes.
```{r accn,fig.height=7,fit.width=8}
nn <- cut2(d$n, c(40, 60, 100, 200, 500))
ggfreqScatter(ac(beta), cstat, by=nn, xlab=xl, ylab=yl)
```
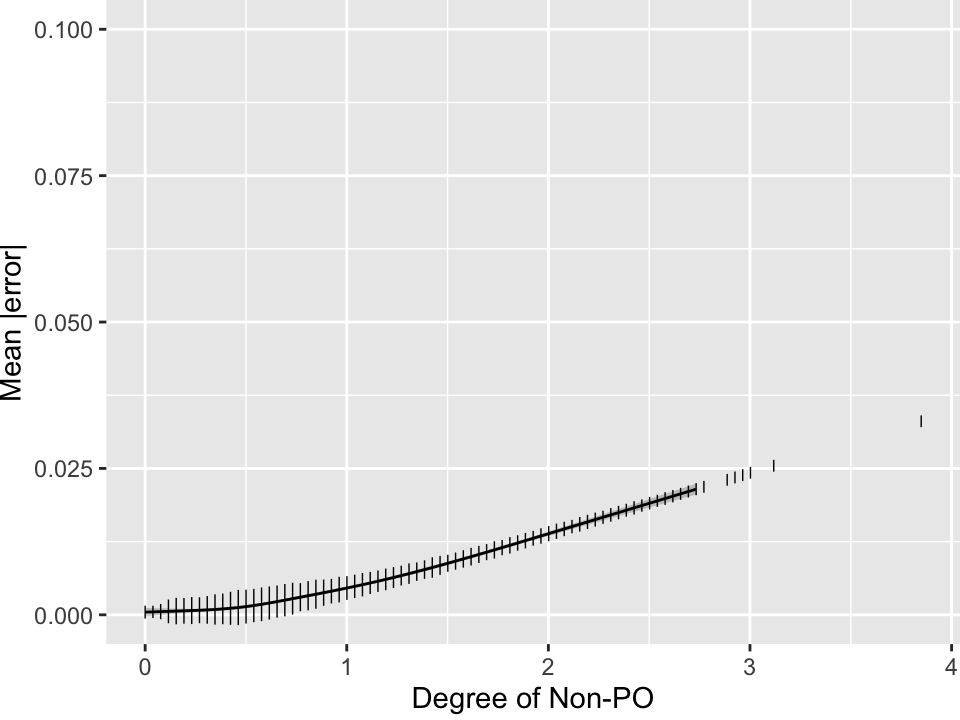
See which version of the non-PO index best predicts the approximation error, and plot the estimated relationship between that index and the MAD.
```{r whichnpo,fig.width=4,fig.height=3.5}
#| fig.width: 5
#| fig.height: 3.75
#| fig.cap: "Mean absolute error in estimating the 0-1 scaled Wilcoxon statistic $c$ from the PO model odds ratio, as a function of the degree of non-PO evident in the sample. The $y$-axis is scaled to $\\frac{1}{10}$th the maximum possible error. Heights of spikes are proportional to the number of simulated trials that had the indicated amount of non-PO after the non-PO metric is split into 100 bins. Gray shaded bands depict 0.95 pointwise confidence intervals for the tenth smallest `npo` to the tenth largest."
r2 <- function(fit) fit$stats['R2']
round(
c('linear npo' = r2(ols(ad ~ npo)),
'spline npo' = r2(ols(ad ~ rcs(npo,5))),
'linear npo2'= r2(ols(ad ~ npo2)),
'spline npo2'= r2(ols(ad ~ rcs(npo2, 5))),
'npo + npo2' = r2(ols(ad ~ rcs(npo, 5) + rcs(npo2, 5)))), 3)
dd <- datadist(npo, npo2); options(datadist='dd')
label(npo) <- 'Degree of Non-PO'
f <- ols(ad ~ rcs(npo, 5))
ggplot(Predict(f), ylab='Mean |error|', xlab='Degree of Non-PO',
rdata=data.frame(npo), ylim=c(0, 0.1),
histSpike.opts=list(frac=function(f) 0.01 + 0.02 * f / (max(f, 2) - 1),
side=1, nint=100))
```
The worst MAD is estimated to be around 0.02 and the relationship steepens around `npo=0.5`. Even though the best model for predicting MAD uses nonlinear functions of both non-PO indexes, for simplicity let's use the stronger of the two, `npo`, for key results.
Earlier plots demonstrate the practical equivalence of the no-covariate PO model and the Wilcoxon test ( $R^{2} = 0.996$ ), as the points hover about the line of identity. Here is a summary of the `r length(worst)` out of `r nrow(d)` simulated trials for which the discrepancy between predicted and actual $c$ was $> 0.075$.
```{r worst}
f <- function(x) sum(duplicated(x))
u <- lapply(worst, function(x)
data.frame(n0=x$n0, n1=x$n1,
Duplicates0=f(x$y0),
Duplicates1=f(x$y1),
npo=round(x$npo, 1),
npo2=round(x$npo2, 1),
`Predicted c`=round(x$pcstat, 2),
`Actual c`=round(x$cstat, 2), check.names=FALSE))
knitr::kable(do.call(rbind, u))
```
The discrepant cases are primarily from smaller unbalanced trials with many ties in Y and non-PO. **Most importantly**, even in the most discrepant datasets there is complete agreement between the PO model and the Wilcoxon test on which group has the higher response tendency, since both approaches yield estimates on the same side of the null values $c=\frac{1}{2}, \beta=0$ in `r sum(agreeDirection)` out of `r length(beta)` trials. The Wilcoxon statistic and the PO model estimate also agree completely in their judgments of equality of treatments. Agreement between $c$ being with $10^{-5}$ of 0.5 and $\hat{\beta}$ being within $10^{-7}$ of 0.0 occurred in `r sum((abs(cstat - 0.5) < 1e-5) == (abs(beta) < 1e-7))` out of `r length(beta)` trials.
::: {`r mNote`}
Note that under the null, PO must hold so no simulations are needed to compute $\alpha$. The null hypothesis implies that the treatment is ineffective everywhere.
:::
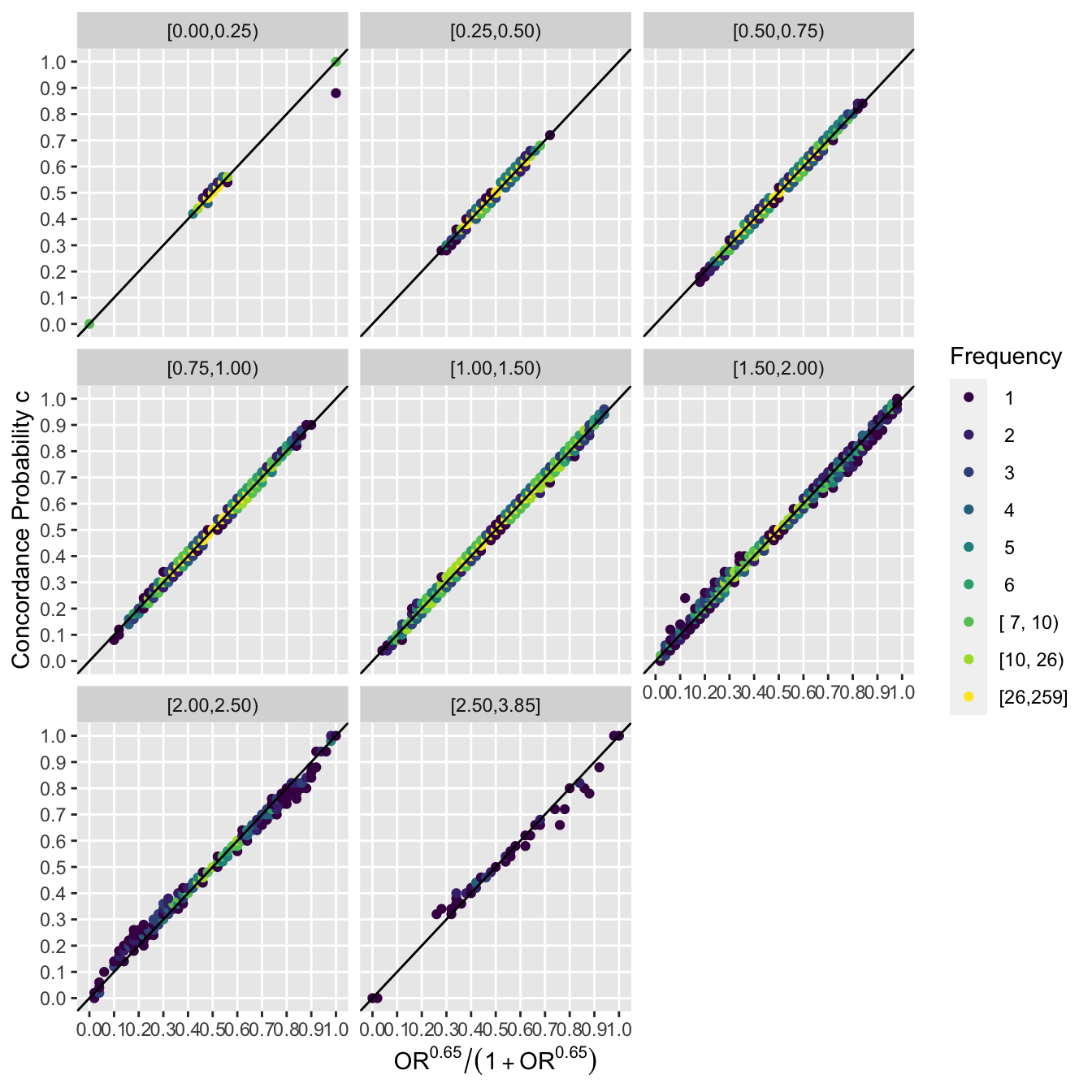
Now go a step further and stratify results by intervals of the non-PO metric.
```{r poscat,fig.height=7,fig.width=7}
by <- cut2(npo, c(.25, .5, .75, 1, 1.5, 2, 2.5))
ggfreqScatter(ac(beta), cstat, by=by, xl=xl, yl=yl) +
geom_abline(intercept=0, slope=1)
```
It can be seen that the extremely tight relationship between the PO OR and the Wilcoxon statistic is unaffected by the amount of non-PO exhibited in the sample.
Repeat these plots using the second non-PO measure.
```{r poscat2,fig.height=7,fig.width=7}
by <- cut2(npo2, c(.25, .5, .75, 1, 1.25, 1.5, 1.75))
ggfreqScatter(ac(beta), cstat, by=by, xl=xl, yl=yl) +
geom_abline(intercept=0, slope=1)
```
To explore the data patterns that corresponded to the strongest PO violations according to the first non-PO measure in the lower right panel here are the logit transformed ECDFs for those `r length(largenpo)` trials. On each panel the total sample size and group allocation ratios are shown. These large non-PO cases are for mainly smaller trials with heavy ties in Y. The first 42 of `r length(largenpo)` trials are shown.
```{r highestnpo,fig.width=6,fig.height=6}
par(mfrow=c(7,6), mar=c(.5,.1,.1,.1), mgp=c(.5, .4, 0))
nt <- min(length(largenpo), 42)
ww <- NULL
for(i in 1 : nt) {
w <- largenpo[[i]]
np <- npod(w$y0, w$y1, pl=TRUE, axes=FALSE, ylim=c(-4,4))
r <- max(c(w$n0 / w$n1, w$n1 / w$n0))
m <- max(w$y0, w$y1)
text(m, -3, paste0('n=', w$n0 + w$n1, ' ratio=', round(r, 1)), adj=1)
if(abs(np[1] - 2.95) < 0.01) ww <- w
}
```
::: {`r mNote`}
Here are details of the simulated trial that resulted in non-PO of 2.95.
```{r highestdetails}
htmlList(ww)
```
:::
# Summary
The unadjusted proportional odds model's odds ratio estimate almost perfectly reflects the Wilcoxon test statistic regardless of the degree of non-proportional odds and sample size. A simple formula $c = \frac{\mathrm{OR}^{0.65}}{1 + \mathrm{OR}^{0.65}}$ allows for conversion between the two, and even under severe non-PO the mean absolute error in estimating $c$ from OR is 0.008. Importantly, the PO results and the Wilcoxon statistic never disagree on the direction of the treatment effect, and they never disagree about the exact equality of treatments, i.e., OR=1.0 if and only if there is complete overlap in the two groups indicated by $c=\frac{1}{2}$ with the Wilcoxon $P$-value being 1.0.
# Further Reading
* <https://hbiostat.org/bib/po>
* <https://hbiostat.org/blog/#category=ordinal>
* [Role of the Proportional Odds Assumption for the Analysis of Ordinal Outcomes in Neurologic Trials](https://www.neurology.org/doi/10.1212/WNL.0000000000214146) by Y Long et al
# Computing Environment
`r markupSpecs$html$session()`